\(\blacktriangleright\) Чтобы найти угол между плоскостями \(\xi\) и \(\pi\), нужно найти линейный угол (причем острый или прямой) двугранного угла, образованного плоскостями \(\xi\) и \(\pi\):

Шаг 1: пусть \(\xi\cap\pi=a\) (линия пересечения плоскостей). В плоскости \(\xi\) отметим произвольную точку \(F\) и проведем \(FA\perp a\);

Шаг 2: проведем \(FG\perp \pi\);

Шаг 3: по ТТП (\(FG\) – перпендикуляр, \(FA\) –наклонная, \(AG\) – проекция) имеем: \(AG\perp a\);

Шаг 4: угол \(\angle FAG\) называется линейным углом двугранного угла, образованного плоскостями \(\xi\) и \(\pi\).

Заметим, что треугольник \(AG\) – прямоугольный.
Заметим также, что плоскость \(AFG\), построенная таким образом, перпендикулярна обеим плоскостям \(\xi\) и \(\pi\). Следовательно, можно сказать по-другому: угол между плоскостями \(\xi\) и \(\pi\) — это угол между двумя пересекающимися прямыми \(c\in \xi\) и \(b\in\pi\), образующими плоскость, перпендикулярную и \(\xi\), и \(\pi\).

Ознакомиться с полной теорией

Задание 8 #1856

Уровень задания: Сложнее ЕГЭ

В кубе \(ABCDA_1B_1C_1D_1\) точка \(K\) лежит на ребре \(AB\), а точка \(L\) лежит на ребре \(CD\), причем \(AK = KB\), \(CL = LD\). Найдите квадрат косинуса двугранного угла между плоскостями \(A_1BC\) и \(A_1KL\).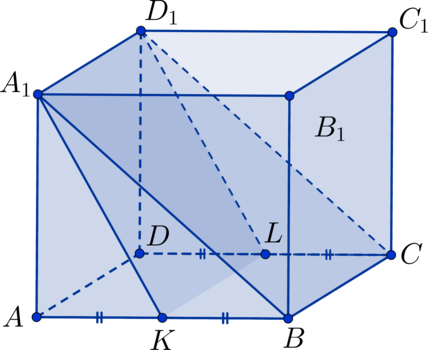

Показать решение

Так как три ребра, выходящие из одной вершины куба, попарно взаимно перпендикулярны, то ребро \(A_1D_1\) перпендикулярно плоскости грани \(AA_1B_1B\) \(\Rightarrow\) \(AA_1B_1 \perp A_1BC\) и \(AA_1B_1 \perp A_1KL\), тогда величина линейного угла \(\angle KA_1B\) совпадает с искомым двугранным углом.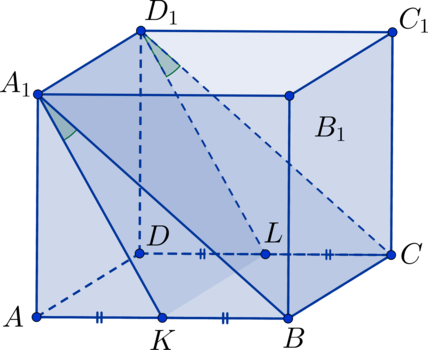

Примем сторону куба за \(x\) и рассмотрим треугольник \(\triangle A_1KB\): \(KB = \frac{1}{2}\cdot AB = \frac{1}{2}x\), \(A_1B\) – диагональ квадрата \(\Rightarrow\) \(A_1B = \sqrt2x\), а сторону \(A_1K\) можно найти по теореме Пифагора из треугольника \(\triangle A_1AK\):

\[A_1K^2 = A_1A^2 + AK^2 = A_1A^2 + (\frac{AB}{2})^2 = x^2 + \frac{x^2}{4} = \frac{5x^2}{4}\ \Rightarrow \ A_1K = \frac{\sqrt5x}{2}.\]

Зная все три стороны в треугольнике \(\triangle A_1KB\), можно воспользоваться теоремой косинусов, чтобы найти косинус искомого угла:

\(KB^2 = A_1K^2 + A_1B^2 - 2\cdot A_1K\cdot A_1B\cdot\cos \angle KA_1B\) \(\Rightarrow\)

\(\frac{x^2}{4} = \frac{5x^2}{4} + 2x^2 - 2\cdot \frac{\sqrt5x}{2}\cdot \sqrt2x\cdot\cos \angle KA_1B\) \(\Rightarrow\)

\(\cos \angle KA_1B = \frac{3}{\sqrt{10}}\) \(\Rightarrow\) \(\cos^2 \angle KA_1B = 0,9\).

Ответ: 0,9

1 2 cледующая
подтема