Задачи по теме «Правильная и прямоугольная пирамиды» (страница 2)

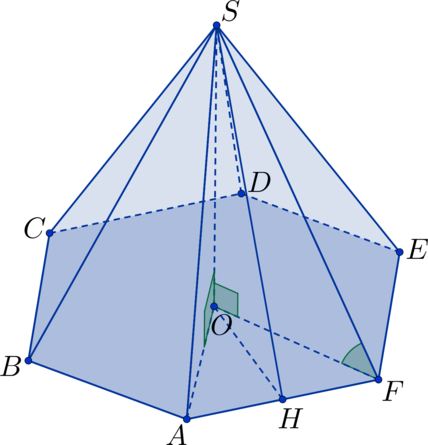
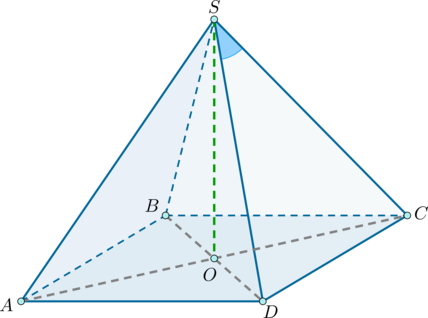
\(SABCDEF\) – правильная шестиугольная пирамида, \(SO\) – высота пирамиды, \(ABCDEF\) – правильный шестиугольник. \(\triangle AOF\) – равносторонний треугольник \(\Rightarrow\) \(FO = 7\). Рассмотрим треугольник \(SOF\): \(SO\) – перпендикуляр, \(SF\) – наклонная к плоскости шестиугольника, \(OF\) – проекция наклонной \(SF\) \(\Rightarrow\) \(\displaystyle \mathrm{tg}\,\angle SFO = \frac{1}{2}\) \(\Rightarrow\) \(\displaystyle SO = FO\cdot\mathrm{tg}\,\angle SFO = \frac{7}{2}\). \(OH\) – высота в равностороннем треугольнике \(\triangle AOF\) \(\Rightarrow\) \(\displaystyle OH = \frac{\sqrt3}{2}\cdot AF = \frac{\sqrt3}{2}\cdot7\). Тогда апофему можно найти из прямоугольного треугольника \(\triangle SOH\) по теореме Пифагора: \(\displaystyle SH^2 = SO^2 + OH^2 = \left(\frac{7}{2}\right)^{2} + \left(\frac{\sqrt3}{2}\cdot7\right)^{2} = 7\).

Ответ: 7

Так как пирамида правильная, то высота \(SO\) падает в точку пересечения медиан (которые являются также высотами и биссектрисами) основания. Пусть \(CK\perp AB\). Тогда \(OK\perp AB\). Тогда по теореме о трех перпендикулярах наклонная \(SK\), проекцией которой является \(OK\), также будет перпендикулярна \(AB\). Следовательно, \(\angle SKC\) – линейный угол двугранного угла при основании, то есть \(\angle SKC=60^\circ\).



Из прямоугольного \(\triangle SKO\): \[\mathrm{tg}\,\angle K=\sqrt3=\dfrac{SO}{OK} \quad\Rightarrow\quad OK=\dfrac{3\sqrt3}{\sqrt3}=3.\] Так как \(OK\) – медиана, а \(O\) – точка пересечения медиан, и медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины, то \(CK=3OK=9\).
Пусть \(KB=x\), тогда \(BC=2x\). Рассмотрим прямоугольный \(\triangle CKB\): \[BC^2=KB^2+CK^2 \quad\Rightarrow\quad 4x^2=x^2+81 \quad\Rightarrow\quad x=3\sqrt3 \quad \Rightarrow\quad BC=6\sqrt3=AB.\] Следовательно, объем пирамиды равен \[V=\dfrac 13\cdot SO\cdot \dfrac 12 AB\cdot CK= \dfrac13\cdot 3\sqrt3\cdot \dfrac12\cdot 6\sqrt3\cdot 9=81.\]

Ответ: 81

Пусть \(SH\) – высота пирамиды. Так как пирамида правильная, то высота падает в центр основания, то есть в точку пересечения медиан (высот, биссектрис).
Заметим, что \(\sqrt{48}=4\sqrt3\).
Пусть \(CC_1\) – высота (а значит и медиана) основания. Тогда \[CC_1=\dfrac{\sqrt3}2AB.\] Так как медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины, то \[CH=\dfrac23CC_1=\dfrac{\sqrt3}3AB.\]
Так как угол между прямой и плоскостью – это угол между прямой и ее проекцией на эту плоскость, а \(CH\) – проекция \(SC\) на плоскость основания, то \(\angle SCH=30^\circ\).
Из прямоугольного \(\triangle SHC\): \[\cos 30^\circ=\dfrac{CH}{SC}\quad\Rightarrow\quad CH=SC\cdot \cos30^\circ \quad\Rightarrow\quad CH=4\sqrt3\cdot \dfrac{\sqrt3}2=6.\] Так как еще \(CH=\dfrac{\sqrt3}3AB\), то можно найти \(AB\): \[6=\dfrac{\sqrt3}3AB \quad\Rightarrow\quad AB=6\sqrt3.\] Также из прямоугольного \(\triangle SHC\): \[\sin30^\circ=\dfrac{SH}{SC} \quad\Rightarrow\quad SH=\dfrac12SC=2\sqrt3.\]
Следовательно, объем пирамиды равен \[V=\dfrac13\cdot SH\cdot S_{ABC}=\dfrac13\cdot 2\sqrt3\cdot \dfrac12\cdot \dfrac{\sqrt3}2\cdot 6\sqrt3\cdot 6\sqrt3=54.\]

Ответ: 54

\(SABCD\) – правильная четырехугольная пирамида. Значит, в ее основании лежит квадрат, а высота \(SO\) пирамиды падает в точку пересечения диагоналей этого квадрата.
\(\angle DSC=\angle CSB=\angle BSA=\angle ASD=60^\circ\), \(AB=6\sqrt2\).

Найдем объем пирамиды, если \(AB=a\), а затем подставим вместо \(a=6\sqrt2\).

Т.к. объем пирамиды равен \[V=\dfrac13 \cdot S_{ABCD}\cdot SO=\dfrac13\cdot a^2\cdot SO,\]

то необходимо найти \(SO\).

\(\triangle CSD\) — равнобедренный (\(SD=SC\)), следовательно, \(\angle D=\angle C=\frac12(180^\circ-60^\circ)=60^\circ\).

Следовательно, он равносторонний и \(SD=SC=CD=a\).

Т.к. \(BD=AB\sqrt2 \quad \Rightarrow \quad OD=0,5BD=\frac{\sqrt2}2\cdot a\).

Тогда по теореме Пифагора из прямоугольного треугольника \(SOD\) (\(\angle SOD=90^\circ\)):

\[SO^2=SD^2-OD^2=a^2-\left(\dfrac{\sqrt2}2\cdot a\right)^2=\dfrac{a^2}2 \quad \Rightarrow \quad SO=\frac{\sqrt2}2\cdot a.\]

Тогда объем равен

\[V=\dfrac13\cdot a^2\cdot \frac{\sqrt2}2\cdot a=\dfrac{a^3}{3\sqrt2}= \dfrac{6^3\cdot 2\sqrt2}{3\sqrt2}=144.\]

Ответ: 144

Построим \(BK\) перпендикулярно \(AC\), как показано на рисунке.

Так как \(BK\) – проекция \(EK\) на плоскость \((ABCD)\), то по теореме о трех перпендикулярах \(EK\) перпендикулярен \(AC\), следовательно, угол между плоскостями \((ABCD)\) и \((ACE)\) есть \(\angle BKE\).

Найдем \(BK\):
рассмотрим параллелограмм \(ABCD\). С одной стороны, его площадь \[S_{ABCD} = ab\cdot\sin 77^{\circ}.\] С другой стороны, его площадь равна удвоенной площади треугольника \(ABC\), то есть \[S_{ABCD} = BK\cdot AC.\] Найдем \(AC\), используя теорему косинусов для треугольника \(ACD\): \[AC^2 = a^2 + b^2 - 2ab\cdot\cos\angle ADC = a^2 + b^2 - 2ab\cdot\cos(180^{\circ} - \angle BCD) = a^2 + b^2 + 2ab\cdot\cos\angle BCD = a^2 + b^2 + 2ab\cdot\cos 77^{\circ},\] откуда \(AC = \sqrt{a^2 + b^2 + 2ab\cdot\cos 77^{\circ}}\).

Приравняв площади параллелограмма, получим: \[ab\cdot\sin 77^{\circ} = BK\cdot\sqrt{a^2 + b^2 + 2ab\cdot\cos 77^{\circ}},\] откуда \[BK = \dfrac{ab\cdot\sin 77^{\circ}}{\sqrt{a^2 + b^2 + 2ab\cdot\cos 77^{\circ}}} = BE,\] тогда треугольник \(BKE\) прямоугольный равнобедренный, откуда \(\angle BKE = 45^{\circ}\).

Ответ: 45

Расстояние от точки до плоскости – длина перпендикуляра, опущенного из этой точки на плоскость.

Так как в основании пирамиды \(GABCDEF\) правильный шестиугольник, то \[S_{ABCDEF} = \dfrac{3\sqrt{3}}{2}a^2\] при \(a = 2\), то есть \[S_{ABCDEF} = 6\sqrt{3}.\]

Тогда суммарная площадь оставшихся граней пирамиды равна \(12 + 6\sqrt{3} - 6\sqrt{3} = 12\). Так как у правильной пирамиды все грани – равные треугольники, то площадь каждой боковой грани равна \(12 : 6 = 2\), откуда с учётом того, что \(AB = 2\) находим высоту треугольника \(ABG\): она равна 2.

Так как \(GABCDEF\) – правильная пирамида, то точка \(O\) – основание перпендикуляра, опущенного из точки \(G\) на плоскость \((ABC)\) – центр описанной около \(ABCDEF\) окружности, \(BO = AO = AB = 2\).

Пусть \(OP\) высота в треугольнике \(ABO\), тогда \(OP = \sqrt{3}\), \(BP = PA\), но треугольник \(ABG\) – равнобедренный, тогда \(GP\) – высота (в нём) и, значит, \(GP = 2\).

По теореме Пифагора \[GO^2 = GP^2 - PO^2 = 4 - 3 = 1,\] откуда \(GO = 1\), то есть расстояние от точки \(G\) до плоскости \((ABC)\) равно 1.

Ответ: 1

Треугольник \(\triangle A_1B_1C\) и \(\triangle ABC\) подобны, т.к. у них общий угол \(\angle C\) и по теореме Фалеса параллельные стороны \(AB\) и \(A_1B_1\) отсекают пропорциональные отрезки. Аналогичным образом подобны треугольники \(\triangle B_1S_1C\) и \(\triangle BSC\). Тогда из пропорциональности соответствующих сторон вытекает подобие треугольников \(\triangle A_1S_1C\), \(\triangle A_1B_1S_1\), соответственно треугольникам \(\triangle ASC\), \(\triangle ABS\). Коэффициент подобия \(k = \frac{B_1C}{BC} = \frac{B_1C}{BB_1 + B_1C} = \frac{1}{4}\). Тогда \(S_{\triangle A_1B_1C}:S_{\triangle ABC} = S_{\triangle A_1S_1C}:S_{\triangle ASC} = S_{\triangle A_1B_1S_1}:S_{\triangle ABS} = S_{\triangle B_1S_1C}:S_{\triangle BSC} = k^2 = \frac{1}{16}\) \(\Rightarrow\) \[\begin{aligned} &S_{\text{пов.}S_1A_1B_1C}:S_{\text{пов.}SABC} = \frac{S_{\triangle A_1B_1C} + S_{\triangle A_1S_1C} + S_{\triangle A_1B_1S_1} + S_{\triangle B_1S_1C}}{S_{\triangle ABC} + S_{\triangle ASC} + S_{\triangle ABS} + S_{\triangle BSC}} = \\[3ex] &= \frac{\frac{1}{16}\cdot S_{\triangle ABC} + \frac{1}{16}\cdot S_{\triangle ASC} + \frac{1}{16}\cdot S_{\triangle ABS} + \frac{1}{16}\cdot S_{\triangle BSC}}{S_{\triangle ABC} + S_{\triangle ASC} + S_{\triangle ABS} + S_{\triangle BSC}} = \\[3ex] &= \frac{\frac{1}{16}\cdot(S_{\triangle ABC} + S_{\triangle ASC} + S_{\triangle ABS} + S_{\triangle BSC})}{S_{\triangle ABC} + S_{\triangle ASC} + S_{\triangle ABS} + S_{\triangle BSC}} = 1:16 \end{aligned}\] \(\Rightarrow\) \(S_{\text{пов.}SABC} = 16\cdot10 = 160\).

Ответ: 160