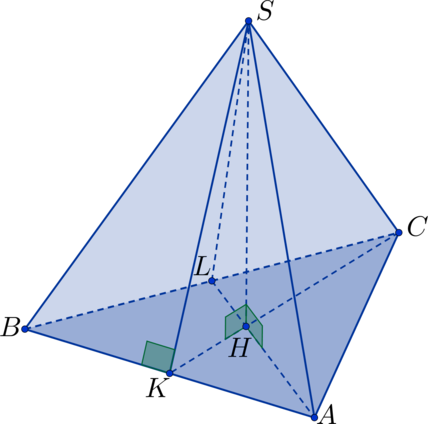
Объем правильной треугольной пирамиды равен \(24\). Найдите объем пирамиды, боковые ребра которой являются апофемами исходной пирамиды.
Пусть \(SKLM\) – пирамида, боковые ребра которой являются апофемами исходной пирамиды \(SABC\). \(SKLM\) тоже является правильной пирамидой, так как вершины треугольника \(\triangle KLM\) являются серединами сторон треугольника \(\triangle ABC\), а значит стороны треугольника \(\triangle KLM\) являются средними линиями треугольника \(\triangle ABC\) \(\Rightarrow\) стороны треугольника \(\triangle KLM\) относятся к соответствующим сторонам треугольника \(\triangle ABC\) как \(1:2\) \(\Rightarrow\) их площади состоят в отношении \(1:4\). Высота искомой пирамиды совпадает с высотой исходной пирамиды \(\Rightarrow\) их объемы относятся также, как их площади \(\Rightarrow\) объем искомой пирамиды равен \(24:4 = 6\).
Ответ: 6