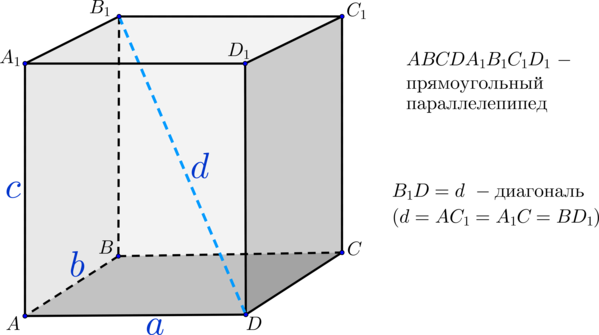
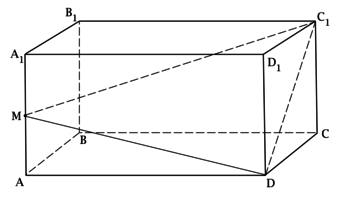
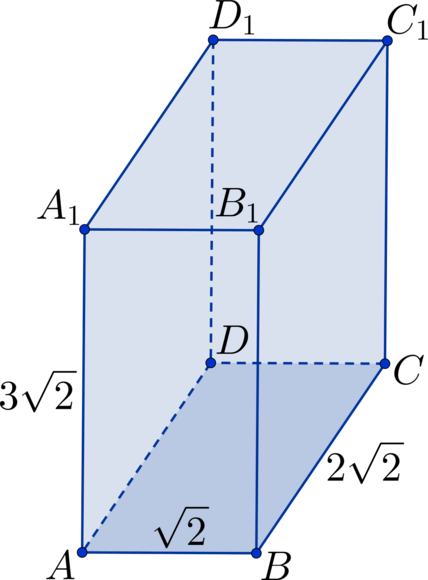
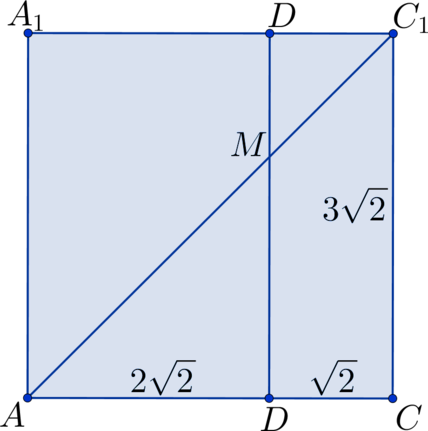
\(ABCDA_1B_1C_1D_1\) – прямоугольный параллелепипед, площадь полной поверхности которого равна 12. Найдите разность между площадью квадрата со стороной \(AA_1 + A_1D_1 + D_1C_1\) и суммой площадей квадратов со сторонами \(AA_1\), \(A_1D_1\), \(D_1C_1\).
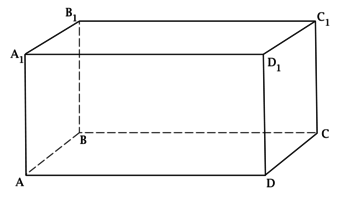
Обозначим \(AA_1 = a\), \(A_1D_1 = b\), \(D_1C_1 = c\), тогда площадь полной поверхности \(ABCDA_1B_1C_1D_1\) равна \[S_{\text{полн}} = 2ab + 2ac + 2bc.\] Площадь квадрата со стороной \(a + b + c\) равна \((a + b + c)^2\), сумма площадей квадратов со сторонами \(a\), \(b\), \(c\) равна \(a^2 + b^2 + c^2\), тогда искомая величина равна
\[\begin{aligned} (a + b + c)^2 - (a^2 + b^2 + c^2) &= a^2 + b^2 + c^2 + 2ab + 2ac + 2bc - (a^2 + b^2 + c^2) =\\ &= 2ab + 2ac + 2bc = S_{\text{полн}} = 12. \end{aligned}\]
Ответ: 12