\(\blacktriangleright\) Признак перпендикулярности прямой и плоскости: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.

\(\blacktriangleright\) Наклонная (к плоскости) \(AB\) – отрезок прямой, не перпендикулярной плоскости, один из концов которого лежит на плоскости (основание наклонной).

\(\blacktriangleright\) Перпендикуляр (к плоскости) \(AA_1\) – отрезок прямой, перпендикулярной плоскости, один из концов которого лежит на плоскости (основание перпендикуляра).

\(\blacktriangleright\) Проекция наклонной \(BA_1\) – отрезок, соединяющий основания перпендикуляра и наклонной.

Теорема о трех перпендикулярах (ТТП):

Пусть в плоскости \(\alpha\) через основание наклонной \(BA\) (т. \(B\,\)) проведена прямая \(a\). Если эта прямая перпендикулярна проекции \(BA_1\) этой наклонной, то она перпендикулярна и самой наклонной.

\(AA_1\perp \alpha; \ a\in \alpha.\) Если \(a\perp BA_1\), то \(a\perp BA\).

Обратная ТТП:

Пусть в плоскости через основание наклонной проведена прямая. Если эта прямая перпендикулярна наклонной, то она перпендикулярна и проекции этой наклонной.

\(AA_1\perp \alpha; \ a\in \alpha.\) Если \(a\perp BA\), то \(a\perp BA_1\).

Ознакомиться с полной теорией

Задание 8 #937

Уровень задания: Сложнее ЕГЭ

Прямые \(a\) и \(b\) перпендикулярны и лежат в плоскости \(\pi\). Прямая \(c\) перпендикулярна прямой \(b\) и пересекает прямую \(a\) в точке \(B\), а также пересекает прямую \(l\) в точке \(C\), так что \(BC = 8\). При этом прямая \(l\) пересекает \(a\) в точке \(A\) так, что \(AB = 6\), \(AC = 10\). Найдите угол между прямыми \(b\) и \(l\). Ответ дайте в градусах.

Показать решение

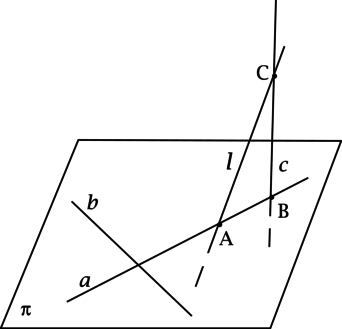
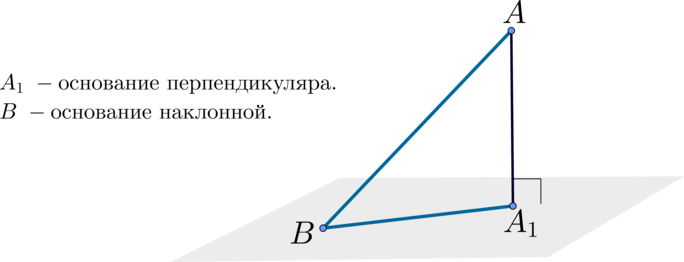
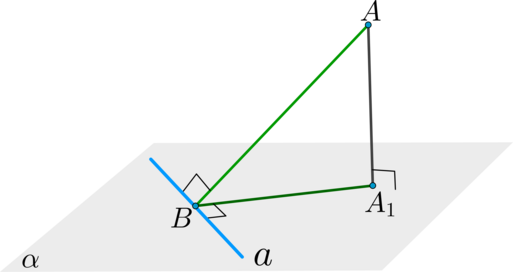
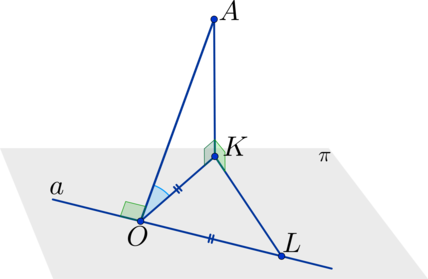
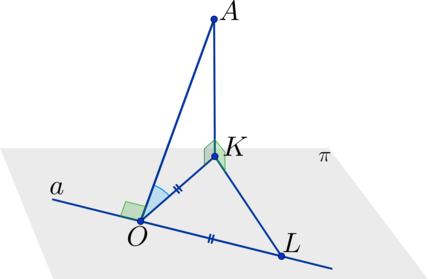
Так как \(AB^2 + BC^2 = AC^2\), то отрезок \(BC\) перпендикулярен \(AB\), следовательно прямая \(c\) перпендикулярна \(a\), но \(c\) перпендикулярна \(b\), \(a\) и \(b\) – пересекаются, тогда \(c\) перпендикулярна \(\pi\), следовательно \(AB\) – проекция \(AC\) на \(\pi\).

Итого: \(b\) перпендикулярна проекции \(l\) на \(\pi\), тогда по теореме о трех перпендикулярах \(b\) перпендикулярна \(l\), то есть угол между ними составляет \(90^{\circ}\).

Ответ: 90

Задание 9 #1852

Уровень задания: Сложнее ЕГЭ

Прямая \(a\) лежит в плоскости \(\pi\), \(AO \perp a\), \(AK\perp\pi\). Точка \(K\) лежит в плоскости \(\pi\), точка \(L\) принадлежит прямой \(a\). Найдите \(AO\), если \(OK=OL\), \(KL = 2\sqrt2\), \(\angle AOK = 60^\circ\).

Показать решение

Т.к. \(AK\) – перпендикуляр к плоскости \(\pi\), \(a\) – прямая в плоскости \(\pi\), а \(AO\) – наклонная, перпендикулярная к прямой \(a\), то согласно теореме о трех перпендикулярах \(KO \perp a\) \(\Rightarrow\) \(\triangle OKL\) – равнобедренный прямоугольный треугольник с прямым углом \(\angle KOL\) \(\Rightarrow\) по теореме Пифагора \(KL^2 = OK^2 + OL^2 = 2\cdot OK^2\) \(\Rightarrow\) \(OK = 2\). В прямоугольном треугольнике \(\triangle AKO\): \(AO = OK : \cos 60^\circ = 2 : \frac{1}{2} = 4\).

Ответ: 4

Задание 10 #1853

Уровень задания: Сложнее ЕГЭ

Прямая \(a\) лежит в плоскости \(\pi\), \(AO \perp a\), \(AK\perp\pi\). Точка \(K\) лежит в плоскости \(\pi\), точка \(L\) принадлежит прямой \(a\). Найдите \(AK\), если \(OK=OL\), \(KL = \sqrt6\), \(\angle AOK = 60^\circ\).

Показать решение

Т.к. \(AK\) – перпендикуляр к плоскости \(\pi\), \(a\) – прямая в плоскости \(\pi\), а \(AO\) – наклонная, перпендикулярная к прямой \(a\), то согласно теореме о трех перпендикулярах \(KO \perp a\) \(\Rightarrow\) \(\triangle OKL\) – равнобедренный прямоугольный треугольник с прямым углом \(\angle KOL\) \(\Rightarrow\) по теореме Пифагора \(KL^2 = OK^2 + OL^2 = 2\cdot OK^2\) \(\Rightarrow\) \(OK = \sqrt3\). В прямоугольном треугольнике \(\triangle AKO\): \(AK = OK \cdot \mathrm{tg}\, 60^\circ = \sqrt3 \cdot \sqrt3 = 3\).

Ответ: 3

1 2 cледующая
подтема