Поиск точек экстремума локального минимума и максимума функций (страница 2)

\(\blacktriangleright\) Если функция задана как частное двух других функций, то \[{\Large{\left(\dfrac fg\right)'=\dfrac{f'\cdot g-f\cdot g'}{g^2}}}\]

\(\blacktriangleright\) Для того, чтобы найти точки экстремума, необходимо схематично изобразить график функции.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания (\(f'>0\)) и убывания (\(f'<0\)) функции, критические точки (где \(f'=0\) или \(f'\) не существует).

\[\begin{array}{|r|c|c|} \hline & \text{Функция } f(x) & \text{Производная } f'(x)\\ \hline \textbf{1} & c & 0\\&&\\ \textbf{2} & x^a & a\cdot x^{a-1}\\&&\\ \textbf{3} & \ln x & \dfrac1x\\&&\\ \textbf{4} & \log_ax & \dfrac1{x\cdot \ln a}\\&&\\ \textbf{5} & e^x & e^x\\&&\\ \textbf{6} & a^x & a^x\cdot \ln a\\&&\\ \textbf{7} & \sin x & \cos x\\&&\\ \textbf{8} & \cos x & -\sin x\\[1ex] \hline \end{array} \quad \quad \quad \quad \begin{array}{|r|c|c|} \hline & \text{Функция } f(x) & \text{Производная } f'(x)\\ \hline \textbf{9} & \mathrm{tg}\, x & \dfrac1{\cos^2 x}\\&&\\ \textbf{10} & \mathrm{ctg}\, x & -\,\dfrac1{\sin^2 x}\\&&\\ \textbf{11} & \arcsin x & \dfrac1{\sqrt{1-x^2}}\\&&\\ \textbf{12} & \arccos x & -\,\dfrac1{\sqrt{1-x^2}}\\&&\\ \textbf{13} & \mathrm{arctg}\, x & \dfrac1{1+x^2}\\&&\\ \textbf{14} & \mathrm{arcctg}\, x & -\,\dfrac1{1+x^2}\\[0.5ex] \hline \end{array}\]

Ознакомиться с полной теорией

Задание 8 #2362

Уровень задания: Сложнее ЕГЭ

Найдите точку минимума функции \(y = \dfrac{2x^3 + 1}{\sqrt[3]{4}x^2}\) на промежутке \((0; 3]\).

Показать решение

ОДЗ: \(x\neq 0\).

1) \[y' = \dfrac{6\sqrt[3]{4}x^4 - 2\sqrt[3]{4}x(2x^3 + 1)}{\sqrt[3]{16}x^4} = \dfrac{2\sqrt[3]{4}(x^3 - 1)}{\sqrt[3]{16}x^3}\]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[\dfrac{2\sqrt[3]{4}(x^3 - 1)}{\sqrt[3]{16}x^3} = 0\qquad\Leftrightarrow\qquad x = 1\,.\] Производная не существует при \(x = 0\).

2) Найдём промежутки знакопостоянства \(y'\):

3) Найдём промежутки знакопостоянства \(y'\) на рассматриваемом промежутке \((0; 3]\):

4) Эскиз графика на промежутке \((0; 3]\):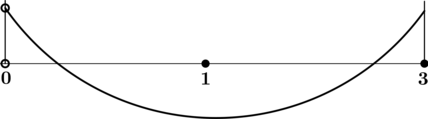

Таким образом, \(x = 1\) – точка минимума функции \(y\) на промежутке \((0; 3]\).

Ответ: 1

1 2 cледующая
подтема