3. Геометрия на плоскости (планиметрия). Часть I
Сумма внутренних углов любого четырехугольника равна \(360^\circ\).
Свойства квадрата:
\(\blacktriangleright\) Те же, что и у ромба и прямоугольника:
\(\sim\) Все стороны равны;
\(\sim\) Диагонали точкой пересечения делятся пополам;
\(\sim\) Все углы прямые;
\(\sim\) Диагонали взаимно перпендикулярны и являются биссектрисами углов квадрата;
\(\sim\) Диагонали равны.
Площадь квадрата
1. Т.к. квадрат является ромбом, то его площадь также равна половине произведения диагоналей.
2. Площадь квадрата равна квадрату его стороны.
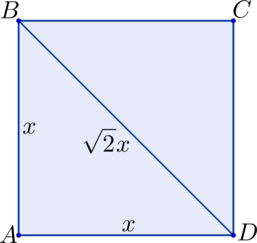
Площадь \(\triangle ABD\) равна \(2\). Найдите периметр квадрата \(ABCD\).
\(S_{ABCD} = 2\cdot S_{\triangle ABD} = 2\cdot2 = 4\). Пусть \(x\) – сторона квадрата, тогда \(x^2 = 4\) \(\Rightarrow\) \(x = 2\) \(\Rightarrow\) \(P_{ABCD} = 4\cdot x = 4\cdot 2 = 8\).
Ответ: 8
Площадь четырехугольника, вершины которого являются серединами сторон квадрата, равна \(1\). Найдите площадь квадрата.
Четырехугольник, вершины которого — середины сторон квадрата, тоже является квадратом, диагонали которого равны сторонам исходного квадрата. Действительно, т.к. \(\triangle A'BB'=\triangle B'CC'=\triangle C'DD'=\triangle D'AA'\), то \(A'B'=B'C'=C'D'=D'A'\), значит, \(A'B'C'D'\) — ромб. Но \(\angle D'A'A=\angle B'A'B=45^\circ\), следовательно, \(\angle D'A'B'=180^\circ-2\cdot 45^\circ=90^\circ\), значит, \(A'B'C'D'\) – квадрат.
\(S_{A'B'C'D'}=\frac12 A'C'^2=1 \Rightarrow A'C'^2=2\). Т.к. \(A'C'=AD\), следовательно, \(S_{ABCD}=AD^2=2\).
Ответ: 2
Периметр четырехугольника, вершины которого являются серединами сторон квадрата равен \(4\sqrt2\). Найдите периметр квадрата.
Четырехугольник, вершины которого – середины сторон квадрата, тоже является квадратом. Тогда сторона внутреннего квадрата равна \(4\sqrt2 : 4 = \sqrt2\) и является средней линией в треугольнике, который отсекается соответствующей диагональю. Значит диагональ внешнего квадрата равна \(2\sqrt2\) \(\Rightarrow\) сторона внешнего квадрата равна \(2\) \(\Rightarrow\) периметр равен \(2\cdot4 = 8\).
Ответ: 8
Периметр \(\triangle ABD\) равен \(16 + 8\sqrt2\). Найдите периметр квадрата \(ABCD\).
Если сторону квадрата обозначить за \(x\), то диагональ квадрата будет равна \(\sqrt 2 x\), тогда \(P_{\triangle ABD} = x + x + \sqrt 2 x = x\cdot(2+\sqrt2) = 16 + 8\sqrt2 = 8\cdot(2 + \sqrt2)\) \(\Rightarrow\) \(x = 8\) \(\Rightarrow\) \(P_{ABCD} = 4\cdot x = 4\cdot8 = 32\).
Ответ: 32
© 2024 Все права защищены | Карта сайта
Политика конфиденциальности
Пользовательское соглашение
