В треугольнике \(ABC\): \(\angle A = 35^{\circ}\), \(BD\) – высота, \(\angle CBD = 26^{\circ}\). Найдите \(\angle ABC\). Ответ дайте в градусах.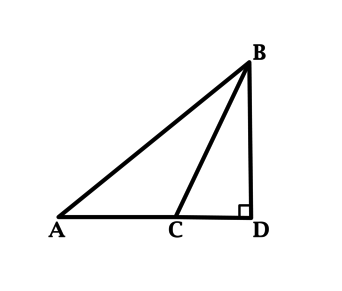
Так как \(BD\) – высота, то \(\angle ADB = 90^{\circ}\). Сумма углов треугольника равна \(180^{\circ}\), тогда \(\angle A + \angle ABD = 180^{\circ} - 90^{\circ} = 90^{\circ}\).
Так как \(\angle ABD = \angle ABC + \angle CBD\), то \(\angle ABD = \angle ABC + 26^{\circ}\). При этом \(\angle A = 35^{\circ}\), тогда \(35^{\circ} + \angle ABC + 26^{\circ} = 90^{\circ}\), откуда находим \(\angle ABC = 29^{\circ}\).
Ответ: 29