3. Геометрия на плоскости (планиметрия). Часть I
Сумма внутренних углов любого четырехугольника равна \(360^\circ\).
Свойства параллелограмма:
\(\blacktriangleright\) Противоположные стороны попарно равны;
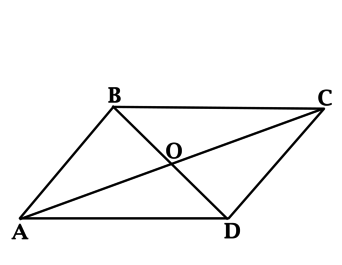
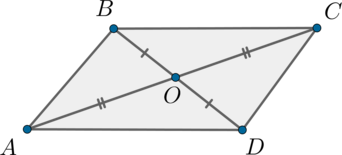
\(\blacktriangleright\) Диагонали точкой пересечения делятся пополам;
\(\blacktriangleright\) Противоположные углы попарно равны, а сумма соседних равна \(180^\circ\).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
\(\blacktriangleright\) если противоположные стороны попарно равны;
\(\blacktriangleright\) если две стороны равны и параллельны;
\(\blacktriangleright\) если диагонали точкой пересечения делятся пополам;
\(\blacktriangleright\) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Площадь параллелограмма равна \(40\), две его стороны равны \(5\) и \(10\). Найдите большую высоту параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена: \(S=ah\). Тогда \(h=S:a\). Следовательно, чем больше \(a\), тем меньше \(h\) (при фиксированном \(S\)). Таким образом, большая высота равна \[h=\dfrac{40}5=8\]
Ответ: 8
Один угол параллелограмма больше другого на \(70^\circ\). Найдите больший угол. Ответ дайте в градусах.
В параллелограмме противоположные углы равны, а прилежащие к одной стороне в сумме дают \(180^\circ\). Следовательно, пусть \(x\) – некоторый угол параллелограмма, тогда второй равен \(x+70^\circ\). Так как они не могут быть противоположными, то они прилежащие к одной стороне, следовательно, \[x+x+70^\circ=180^\circ\quad\Rightarrow\quad x=55^\circ\] Тогда больший угол параллелограмма равен \(x+70^\circ=125^\circ\).
Ответ: 125
Периметр треугольника равен 6. Найдите периметр треугольника, стороны которого параллельны сторонам данного и проходят через его вершины.
Пусть длины сторон треугольника \(ABC\): \(AB, BC, CA\) равны \(a, b, c\) соответственно, тогда периметр треугольника \(ABC: P_{ABC} = a + b + c\). Найдем сторону \(EF\): из условия известно, что \(EF\parallel AB, DE\parallel AC, DF\parallel BC\), тогда можно заметить, что четырёхугольники \(ABCF\) и \(ABEC\) – параллелограммы, т. к. стороны этих четырёхугольников попарно параллельны. По свойству параллелограмма противоположные стороны попарно равны, а значит, что \(AB=FC=CE\Rightarrow EF = 2\cdot a\), аналогично доказывается, что: \[DE = 2\cdot c, DF = 2\cdot b\Rightarrow P_{DEF} = 2\cdot (a+b+c) = 2\cdot P_{ABC} = 12.\]
Ответ: 12
В параллелограмме \(ABCD\) сумма длин диагоналей равна 10, а меньшая сторона параллелограмма \(ABCD\) равна 2. Найдите наименьший из периметров треугольников, на которые диагонали делят параллелограмм \(ABCD\).
В параллелограмме диагонали пересекаются и точкой пересечения делятся пополам. Пусть точка пересечения диагоналей – точка \(O\), тогда \(AO + BO = 0,5(AC + BD) = 5 = AO + OD = OD + OC = OC + OB\).
Таким образом, периметр каждого из треугольников, на которые диагонали делят параллелограмм \(ABCD\), равен полусумме диагоналей параллелограмма \(ABCD\) плюс сторона параллелограмма, которая является стороной этого треугольника.
Тогда наименьшим будет периметр того из этих треугольников, стороной которого является одна из меньших сторон параллелограмма и равен он \(5 + 2 = 7\).
Ответ: 7
Две вершины квадрата расположены на гипотенузе равнобедренного прямоугольного треугольника, а две другие – на катетах. Найдите сторону квадрата, если гипотенуза равна 9.
Т.к. треугольник равнобедренный и прямоугольный, то его углы при гипотенузе равны по \(45^\circ\). Квадрат образует с гипотенузой углы \(\angle GFC = 90^\circ\) и \(\angle DEF = 90^\circ\), а значит, что треугольники \(DBE\) и \(GFC\) – равнобедренные прямоугольные, т.к. \(\angle BDE = 45^\circ, \angle FGC = 45^\circ\). Пусть сторона квадрата равна \(a\), тогда длину гипотенузы можно выразить через сторону квадрата: \[BC = 3\cdot a = 9\Rightarrow a = 3.\]
Ответ: 3
Диагонали параллелограмма \(ABCD\) пересекаются в точке \(O\). Периметр параллелограмма равен 12, а разность периметров треугольников \(BOC\) и \(COD\) равна 2. Найдите большую сторону параллелограмма.
По свойству параллелограмма: диагонали точкой пересечения делятся пополам, т.е. \(BO = DO, AO = CO.\) \[P_{BOC} = BC + BO + CO, P_{COD} = CD + DO + CO \Rightarrow P_{BOC} - P_{COD} = BC - CD = 2.\] Пусть \(BC = x\), тогда \(CD = x - 2\), подставим эти выражения в формулу периметра: \[BC + AD + CD + AB = x+x+(x-2)+(x-2) = 12\Rightarrow x = 4.\]
Ответ: 4
Найдите периметр четырехугольника с вершинами в серединах сторон прямоугольника с диагональю, равной 8.
Пусть \(AB = a, BC = b\), в прямоугольнике все углы прямые, тогда по теореме Пифагора: \[\sqrt{a^2 + b^2} = 8.\] Найдем сторону \(EF\): т.к. \(E\) и \(F\) – середины сторон \(AB\) и \(BC\), то \(BF = \dfrac{b}2, EB = \dfrac{a}2\), тогда \(EF = \sqrt{\dfrac{a^2}4 + \dfrac{b^2}4}\), аналогично находятся остальные стороны, которые равны. Найдем периметр: \[P_{EFGK} = 4\cdot \sqrt{\dfrac{a^2}4 + \dfrac{b^2}4} = 2\cdot\sqrt{a^2 + b^2} = 2\cdot AC = 16.\]
Ответ: 16
