3. Геометрия на плоскости (планиметрия). Часть I
Биссектриса параллелограмма — это отрезок, соединяющий вершину параллелограмма с точкой на одной из двух противоположных сторон и делящий угол при вершине пополам.
\(\bullet\) Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
\(\bullet\) Биссектрисы соседних углов параллелограмма взаимно перпендикулярны: \(BL\perp AN\).
\(\bullet\) Биссектрисы противоположных углов параллелограмма параллельны: \(AN\parallel CP\).
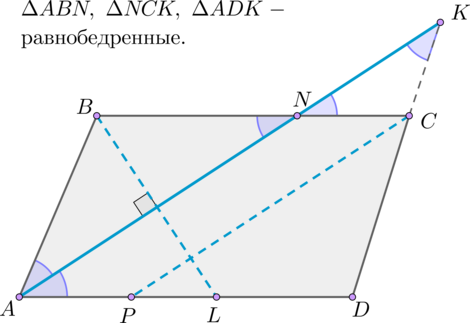
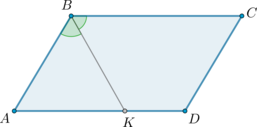
В параллелограмме \(ABCD\): \(BK\) – биссектриса, \(BK = AK\). Чему равен \(\angle D\)?
Т.к. биссектриса отсекает равнобедренный треугольник от параллелограмма, то \(AK = AB\). Значит \(\triangle ABC\) равносторонний \(\Rightarrow\) \(\angle A = 60^\circ\) \(\Rightarrow\) \(\angle D = 180^\circ - 60^\circ = 120^\circ\).
Ответ: 120
В параллелограмме \(ABCD\) проведены биссектрисы \(AN\) и \(BE\) односторонних углов. Найдите \(BE\), если \(AN=16\), \(AB=10\).
По свойству биссектрисы параллелограмма \(\triangle ABE\) и \(\triangle
ABN\) – равнобедренные, то есть \(AE=AB=BN\). Следовательно, \(AO\) – биссектриса, проведенная к основанию, значит, высота, то есть \(\angle AOB=90^\circ\), а также и медиана, то есть \(BO=OE\). Аналогично \(AO=ON=\frac12AN=8\). Тогда по теореме Пифагора из \(\triangle AOB\): \[BO=\sqrt{AB^2-AO^2}=6 \quad\Rightarrow\quad BE=2\cdot 6=12.\]
Ответ: 12
В параллелограмме \(ABCD\): \(BC = 2\cdot AB\), \(AN\) и \(CM\) – биссектрисы, \(AB = 4\). Найдите \(NM\).
Внутренние накрест лежащие углы при параллельных прямых и секущей равны, тогда \(\angle BNA = \angle NAD\), но \(\angle NAD = \angle BAN\), тогда \(\angle BNA = \angle BAN\) и треугольник \(BAN\) – равнобедренный, \(AB = BN\). Обозначим \(AB = x\).
Аналогично треугольник \(MCD\) – равнобедренный, \(x = CD = MD\).
\(BC = 2x = AD\), тогда \(NC = x = AM\), следовательно, \(BN = x = AM\); \(AM \parallel BN\), тогда \(ABNM\) – параллелограмм, откуда заключаем, что \(MN = AB = 4\).
Ответ: 4
В параллелограмме \(ABCD\) биссектрисы \(BK\) и \(AL\) пересекаются в точке \(O\). Найдите периметр параллелограмма \(ABCD\), если \(AD = 10\), а медиана \(OM\) в \(\triangle AOB\) равна \(4\).
\(\angle AOB = 90^\circ\) \(\Rightarrow\) \(OM = \frac{1}{2}\cdot AB\), т.к. в прямоугольном треугольнике медиана, проведенная из прямого угла, равна половине гипотенузы. Тогда \(AB = 2\cdot 4 = 8\) \(\Rightarrow\) \(P_{ABCD} = 2\cdot8 + 2\cdot10 = 36\).
Ответ: 36
В трапеции \(ABCD\) с основаниями \(AD\) и \(BC\) проведены биссектрисы углов \(A\) и \(B\), пересекающие основания соответственно в точках \(N\) и \(K\). Найдите периметр четырехугольника \(ABNK\), если \(AB=5\).
(Задача от подписчиков)
\(\angle AKB=\angle KBN\) как накрест лежащие при \(AD\parallel BC\) и \(BK\) секущей. Следовательно, \(\angle AKB=\angle ABK\), следовательно, \(\triangle BAK\) равнобедренный. Отсюда \(AB=AK=5\).
Аналогично, \(\angle BNA=\angle NAK=\angle NAB\), следовательно, \(\triangle ABN\) – равнобедренный. Отсюда \(AB=BN=5\).
Заметим, что \(AK=BN=5\) и \(AK\parallel BN\), следовательно, по признаку \(ABNK\) – параллелограмм. Следовательно, \(NK=AB=5\). Следовательно, периметр \(ABNK\) равен \(5+5+5+5=20\).
Ответ: 20
Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
Проведем биссектрисы двух соседних углов. Пусть они разбили первый угол на два угла, равных \(x\), второй угол — на два угла, равных \(y\). Нужно найти \(\alpha\).
По свойству параллелограмма сумма его углов, прилежащих к одной стороне, равна \(180^\circ\). Следовательно, \(2x+2y=180^\circ\), или \(2(x+y)=180^\circ\), откуда \(x+y=90^\circ\).
Так как сумма углов в треугольнике равна \(180^\circ\), то \(x+y+\alpha=180^\circ\), откуда \(\alpha=180^\circ-(x+y)=180^\circ-90^\circ=90^\circ\).
Ответ: 90
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении \(4:3\), считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен \(88\).
Из условия задачи следует, что \(AK:KD=4:3\). Обозначим \(AK=4x\), \(KD=3x\). Следовательно, \(AD=7x\).
Так как в параллелограмме противоположные стороны параллельны, то \(\angle AKB=\angle KBC\) как накрест лежащие при \(AD\parallel BC\) и секущей \(BK\). Следовательно, \(\angle AKB=\angle ABK\), то есть \(\triangle ABK\) равнобедренный: \(AK=AB\). Отсюда \(AB=4x\).
Следовательно, периметр \(88=2(4x+7x)\) (так как противоположные стороны параллелограмма равны), следовательно, \(x=4\).
Значит, большая сторона параллелограмма равна \(7x=28\).
Ответ: 28
