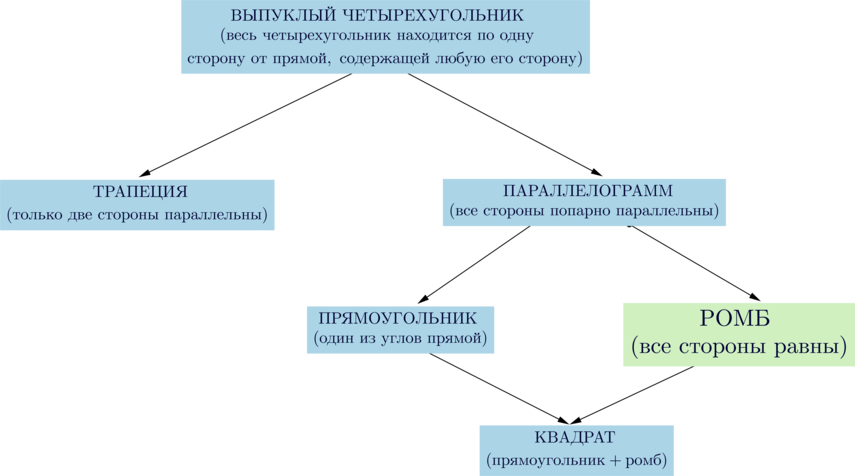
Середины сторон ромба \(ABCD\) являются вершинами четырехугольника \(KLMN\). Середины сторон \(KLMN\) — четырехугольника \(PQRS\). Найдите отношение площади ромба \(ABCD\) к площади четырехугольника \(PQRS\)?
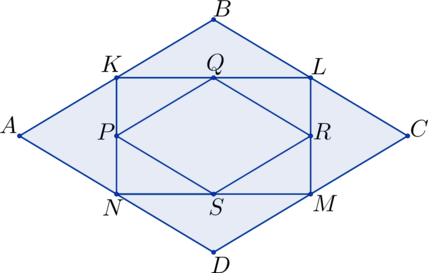
1) По теореме Вариньона \(KLMN\) – параллелограмм. Но т.к. \(KN\parallel BD, KL\parallel AC, BD\perp AC \ \Rightarrow \ KN\perp KL\), значит, \(KLMN\) — прямоугольник, причем \(S_{KLMN}=KN\cdot KL\).
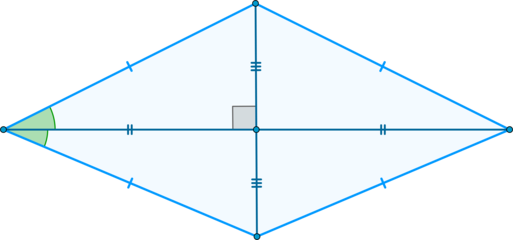
Т.к. площадь ромба равна полупроизведению диагоналей, то \(S_{ABCD}=\frac12 AC\cdot BD\). Но \(KN=\frac12 BD, KL=\frac12 AC\) как средние линии, следовательно, \(S_{ABCD}=\frac12 AC\cdot BD=2KN\cdot KL=2\cdot S_{KLMN}\).
2) Аналогично \(PQRS\) – параллелограмм. Но, как средние линии, \(PQ=\frac12NL, PS=\frac12 KM\); а \(NL=KM\), значит и \(PQ=PS\). Следовательно, \(PQRS\) – ромб.
Заметим, что \(QS=KN, PR=KL\), значит, \(S_{PQRS}=\frac 12 QS\cdot PR=\frac 12 KLMN\).
Из всего этого следует, что \(S_{ABCD}=4S_{PQRS}\). Значит, отношение равно \(4\).
Ответ: 4