3. Геометрия на плоскости (планиметрия). Часть I
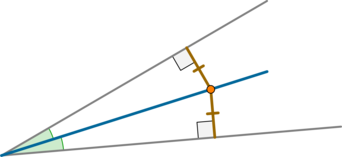
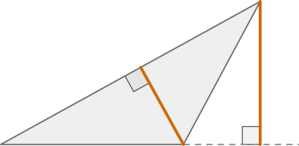
\(\blacktriangleright\) Высота треугольника может упасть как на сторону, так и на ее продолжение. Второй случай возможен только если треугольник тупоугольный и высота проведена из вершины острого угла.
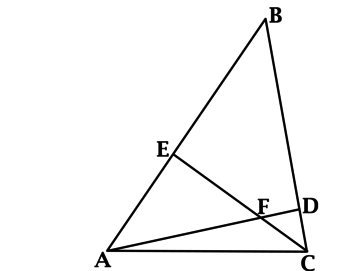
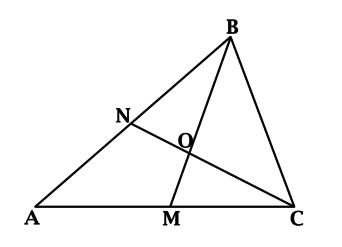
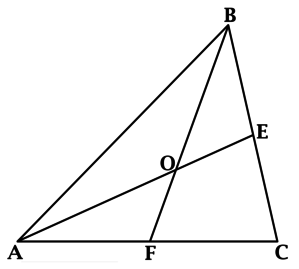
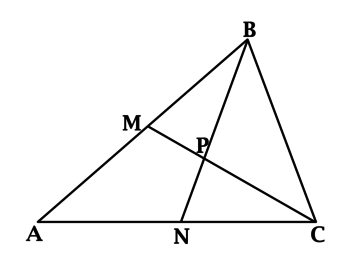
\(\blacktriangleright\) Все медианы треугольника пересекаются в одной точке.
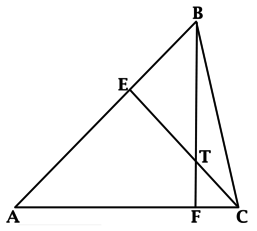
Все высоты (или их продолжения) пересекаются в одной точке.
Все биссектрисы пересекаются в одной точке.
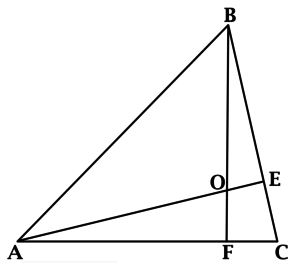
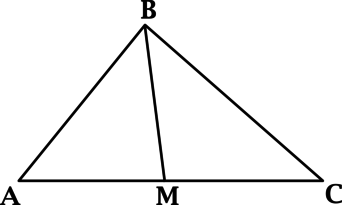
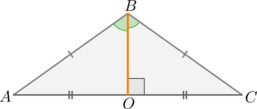
\(\blacktriangleright\) В равнобедренном треугольнике биссектриса, высота и медиана, проведенные к основанию, совпадают (отрезок \(BO\,\)).
Обратно: если в треугольнике совпадают биссектриса и медиана (биссектриса и высота, высота и медиана), проведенные к одной стороне, то этот треугольник равнобедренный.
\(\blacktriangleright\) В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Обратно: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.
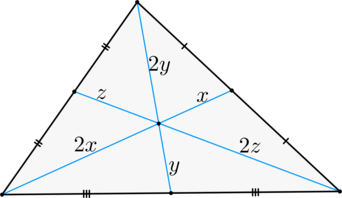
\(\blacktriangleright\) Медианы треугольника своей точкой пересечения делятся в отношении \(2:1\), считая от вершины.
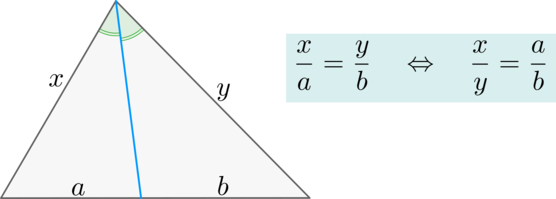
\(\blacktriangleright\) Биссектриса треугольника делит сторону, к которой она проведена, на отрезки, пропорциональные прилежащим сторонам.
Обратно: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.
\(\blacktriangleright\) Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Обратно: каждая точка биссектрисы угла равноудалена от его сторон.
В треугольнике \(ABC\): \(CE\) и \(BF\) – высоты, пересекающиеся в точке \(T\), \(\angle ETB = 31^{\circ}\). Найдите \(\angle A\). Ответ дайте в градусах.
\(\angle FTE = 180^{\circ} - \angle ETB = 149^{\circ}\).
\(\angle A + \angle AET + \angle AFT + \angle FTE = 360^{\circ}\), откуда \(\angle A + 90^{\circ} + 90^{\circ} + 149^{\circ} =
360^{\circ}\), следовательно, \(\angle A = 31^{\circ}\).
Ответ: 31
В треугольнике \(ABC\): \(\angle A = 60^{\circ}\), \(\angle C = 80^{\circ}\), \(AD\) и \(CE\) – высоты, пересекающиеся в точке \(F\). Найдите \(\angle EFD\). Ответ дайте в градусах.
Треугольник \(AEC\) – прямоугольный, \(\angle A = 60^{\circ}\), тогда \(\angle ACE = 90^{\circ} - 60^{\circ} = 30^{\circ}\). Аналогично в треугольнике \(ADC\) находим, что \(\angle DAC = 10^{\circ}\).
Так как сумма углов треугольника равна \(180^{\circ}\), то \(\angle AFC = 180^{\circ} - 10^{\circ} - 30^{\circ} = 140^{\circ}\). Углы \(AFC\) и \(EFD\) равны как вертикальные, тогда \(\angle EFD = 140^{\circ}\).
Ответ: 140
В треугольнике \(ABC\): \(AE\) и \(BF\) – высоты, пересекающиеся в точке \(O\), \(\angle FBC = 19^{\circ}\). Найдите \(\angle FOE\). Ответ дайте в градусах.
Треугольник \(BOE\) – прямоугольный, \(\angle OBE = 19^{\circ}\), тогда \(\angle BOE = 90^{\circ} - 19^{\circ} = 71^{\circ}\). \(\angle FOE\) – смежный с \(\angle BOE\), тогда их сумма равна \(180^{\circ}\) и, значит, \(\angle FOE = 109^{\circ}\).
Ответ: 109
В треугольнике \(ABC\): \(BM\) и \(CN\) – медианы, \(BM = CN\), \(O\) – точка пересечения \(BM\) и \(CN\), \(\angle OBC = 36^{\circ}\). Найдите \(\angle BOC\). Ответ дайте в градусах.
В треугольнике медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины. Так как \(BM = CN\), то \(BO = \dfrac{2}{3}BM = \dfrac{2}{3}CN = CO\), тогда треугольник \(BOC\) – равнобедренный. В равнобедренном треугольнике углы при основании равны, тогда \(\angle OCB = \angle OBC = 36^{\circ}\).
Так как сумма углов в треугольнике равна \(180^{\circ}\), то \(\angle BOC = 180^{\circ} - \angle OBC - \angle OCB = 180^{\circ} - 36^{\circ} - 36^{\circ} = 108^{\circ}\).
Ответ: 108
В треугольнике \(ABC\): \(BF\) и \(AE\) – медианы, \(AE = BF\), \(O\) – точка пересечения \(BF\) и \(AE\), \(\angle FOE = 147^{\circ}\). Найдите \(\angle ABO\). Ответ дайте в градусах.
\(\angle AOB = \angle FOE = 147^{\circ}\) (как вертикальные).
В треугольнике медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины. Так как \(AE = BF\), то \(AO = \dfrac{2}{3}AE = \dfrac{2}{3}BF = BO\), тогда треугольник \(ABO\) – равнобедренный. В равнобедренном треугольнике углы при основании равны, тогда \(\angle OAB = \angle ABO\).
Так как сумма углов в треугольнике равна \(180^{\circ}\), то \(180^{\circ} = \angle OAB + \angle ABO + \angle AOB = 2\cdot \angle ABO + 147^{\circ}\), откуда \(\angle ABO = 16,5^{\circ}\).
Ответ: 16,5
В треугольнике \(ABC\): \(BM\) – биссектриса, причем \(AM = 3\), \(MC = 5\), \(BC = 10\). Найдите \(AB\).
По теореме о биссектрисе (биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам) имеем: \(\dfrac{AB}{AM} = \dfrac{BC}{MC}\), тогда \(\dfrac{AB}{3} = \dfrac{10}{5} = 2\), откуда \(AB = 6\).
Ответ: 6
В треугольнике \(ABC\): \(BN\) и \(CM\) – медианы, \(P\) – точка пересечения \(BN\) и \(CM\), \(\angle PBC = 35^{\circ}\), \(\angle BPC = 110^{\circ}\), \(AB = 4\). Найдите \(NC\).
Так как сумма углов в треугольнике равна \(180^{\circ}\), то \(\angle PCB = 180^{\circ} - 110^{\circ} - 35^{\circ} = 35^{\circ} = \angle PBC\), значит, треугольник \(PBC\) – равнобедренный и \(PB = PC\).
В треугольнике медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины. Так как \(PB = PC\), то \(MP = 0,5\cdot PC = 0,5 \cdot PB = PN\).
\(\angle MPB\) и \(\angle NPC\) – вертикальные, а значит, равные.
Таким образом, треугольники \(MPB\) и \(PNC\) – равны (по двум сторонам и углу между ними), тогда \(NC = MB = 0,5\cdot AB = 2\).
Ответ: 2
