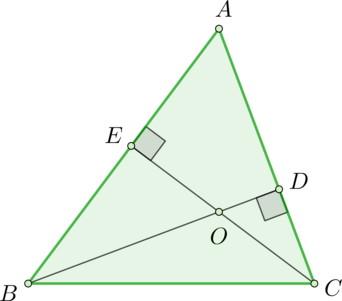
В треугольнике \(ABC\) угол \(A\) равен \(56^\circ\), углы \(B\) и \(C\) – острые. Высоты \(BD\) и \(CE\) пересекаются в точке \(O\). Найдите угол \(DOE\). Ответ дайте в градусах.
1 способ
Проведем \(OA\).
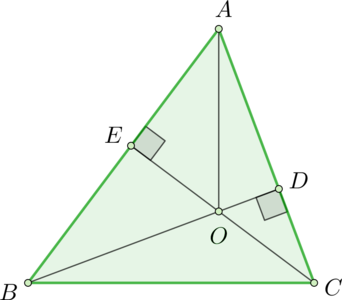
Тогда \(\angle DOE=\angle DOA+\angle EOA\). Так как \(\angle AEO=\angle
ADO=90^\circ\), то из прямоугольных треугольников \(\triangle AEO\) и \(\triangle ADO\) \(\angle EOA=90^\circ-\angle OAE\), \(\angle
DOA=90^\circ-\angle OAD\). Следовательно: \[\angle DOE=\angle DOA+\angle EOA=90^\circ-\angle OAD+90^\circ-\angle OAE=
180^\circ-(\angle OAD+\angle OAE)=180^\circ-\angle
A=180^\circ-56^\circ=124^\circ\]
2 способ
Вспомним, что сумма углов выпуклого четырехугольника равна \(360^\circ\). Тогда для четырехугольника \(AEOD\): \(\angle A+\angle E+\angle O+\angle D=360^\circ\), откуда \[\angle DOE=\angle O=360^\circ-90^\circ-90^\circ-56^\circ=124^\circ\]
Ответ: 124