Задачи на нахождение площади и периметра треугольника (страница 3)

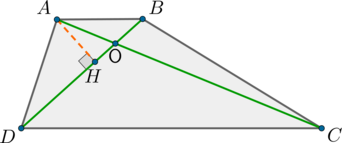
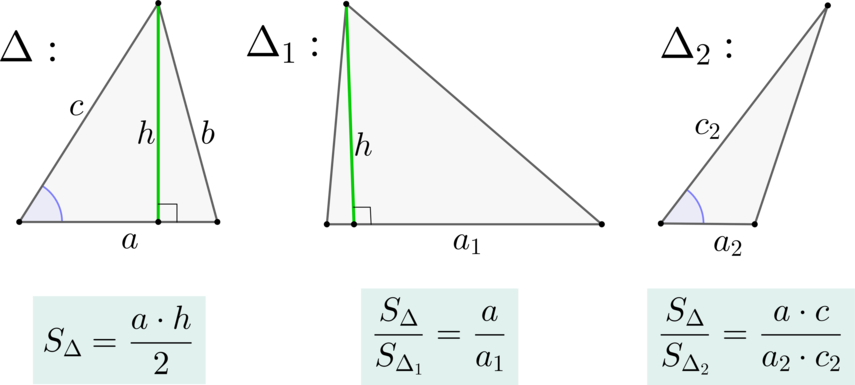
По формуле площади треугольника:

\[S_{ADO} = 0,5\cdot 2BO\cdot OH\Rightarrow S_{AOB} = 0,5\cdot BO\cdot OH =12 : 2 = 6.\]

Т.к. \(AB\parallel DC\Rightarrow \) треугольники \(AOB\) и \(DOC\) подобны и коэффициент подобия:

\[k = \dfrac{DO}{BO} = 2\Rightarrow \dfrac{S_{DOC}}{S_{AOB}}= k^2 = 4.\] \[S_{DOC} = 6\cdot 4 =24, S_{BOC} = S_{AOD} = 12.\] \[S_{ABCD} = S_{AOD} + S_{AOB} + S_{DOC} + S_{BOC} = 54.\]

Ответ: 54

Пусть \(BP\) и \(BQ\) - высота и биссектриса данного треугольника \(ABC\) соответственно. По формуле Герона:

\[S_{ABC} = \sqrt{42\cdot(42 - 30)(42 - 28)(42 - 26)}=14\cdot6\cdot4 = 336.\]

Запишем формулу площади треугольника \(ABC\) через высоту: \(S_{ABC} = \dfrac{AC\cdot BP}2\). Тогда

\[BP = \dfrac{2\cdot S_{ABC}}{AC} = \dfrac{2\cdot 336}{28} = 24.\]

Из свойства биссектрисы треугольника: \(\dfrac{AQ}{QC} = \dfrac{AB}{BC} = \dfrac{13}{15}.\)

Поэтому: \(AQ = \dfrac{13}{28}\cdot AC =13.\)

По теореме Пифагора из прямоугольного треугольника \(APB\):

\[AP = \sqrt{AB^2-BP^2} = \sqrt{26^2-24^2} = 10.\]

Слeдовательно, \(PQ = AQ - AP = 13-10=3, S_{BPQ} = \dfrac{1}2 \cdot PQ \cdot BP = \dfrac{3\cdot 24}2 = 36.\)

Ответ: 36

Треугольники \(ABC\) и \(HBC\) имеют общий угол \(B\), следовательно:

\[\dfrac{S_{HBC}}{S_{ABC}} = \dfrac{HB\cdot BC}{AB\cdot BC} = \dfrac{HB}{AB}.\]

Пусть \(HB = 2x\), \(AH = 3x\), учитывая то, что \(AB = HB + AH\), получаем:

\[\dfrac{HB}{AB} = \dfrac{2x}{2x+3x} = \dfrac{2}5 \quad\Rightarrow \quad S_{HBC} = S_{ABC} \cdot \dfrac{2}5 = 6.\]

Ответ: 6

Биссектриса делит треугольник \(ABC\) на два треугольника, имеющие по равному углу, следовательно, их площади относятся как произведения сторон, образующих эти углы:

\[\dfrac{S_{ABD}}{S_{DBC}} = \dfrac{AB\cdot BD}{BC\cdot BD} = \dfrac{AB}{BC}\quad (*)\] Площадь треугольника \(BDC\) равна

\[S_{DBC} = \dfrac{1}2\cdot DH\cdot BC = \dfrac{1}2\cdot 3\cdot 6 = 9.\] Найдем площадь треугольника \(ABD\) из отношения \((*)\):

\[S_{ABD} = \dfrac{4}6\cdot S_{DBC} = \dfrac{4}6\cdot 9 = 6.\] Сложим площади треугольников \(ABD\) и \(DBC\) и получим площадь искомого треугольника \(ABC\):

\[S_{ABC} = S_{ABD} + S_{DBC} = 6 + 9 =15.\]

Ответ: 15

Так как \(AC\) перпендикулярна прямой \(BC\), то \(AC\) – высота тупоугольного треугольника \(ABD\), опущенная из вершины \(B\) на продолжение стороны \(BD\). Так как площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию, то \[S_{ABD}=\dfrac12\cdot BD\cdot AC=\dfrac12\cdot 4\cdot 5=10\]

Ответ: 10

Медиана \(DB\) делит \(KA\) пополам \(\Rightarrow KB = 5\). Так как известны все стороны треугольника \(KDB\), найдем его площадь по формуле Герона: \[S_{KDB} = \sqrt{6\cdot(6 - 3)(6 - 4)(6 - 5)}=6.\] Медиана треугольника делит его на два равновеликих треугольника, то есть \(S_{KDB}=S_{ADB}\), следовательно,

\[S_{KDA} = 2\cdot S_{KDB} = 12.\]

Ответ: 12

По свойству биссектрисы: \[\dfrac{TC}{BC} = \dfrac{AT}{AB}\] Пусть \(BC = x, AB = y\), тогда: \[\dfrac{12}x = \dfrac{15}y\Rightarrow x = 0,8\cdot y.\] Из треугольника \(ABC\) имеем по теореме Пифагора: \(x^2+27^2 = y^2\Rightarrow 0,64\cdot y^2 + 27^2 = y^2\Rightarrow y = 45, x = 36.\) \[S_{ABT} = 0,5\cdot AT\cdot BC = 0,5\cdot 15\cdot 36 = 270.\]

Ответ: 270