В треугольнике \(ABC\): \(AB = BC\), \(AD\) – высота, \(\angle CAD = 19^{\circ}\). Найдите \(\angle B\). Ответ дайте в градусах.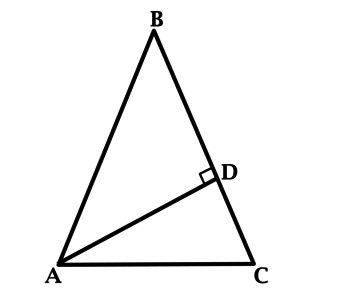
Так как \(AD\) – высота, то \(\angle CDA = 90^{\circ}\), тогда \(\angle CAD + \angle C = 90^{\circ}\). \(\angle CAD = 19^{\circ}\), тогда \(\angle C = 71^{\circ}\).
В равнобедренном треугольнике углы при основании равны, тогда \(\angle CAB = \angle C = 71^{\circ}\). Сумма углов треугольника равна \(180^{\circ}\), тогда \(\angle B = 180^{\circ} - \angle C - \angle CAB = 180^{\circ} - 71^{\circ} - 71^{\circ} = 38^{\circ}\).
Ответ: 38