В треугольнике \(ABC\): \(\angle A = 51^{\circ}\), \(\angle C = 77^{\circ}\), \(BD\) – биссектриса, \(P\) – такая точка на \(AB\), что \(PB = BC\). Найдите \(\angle ADP\). Ответ дайте в градусах.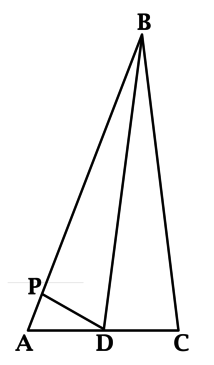
Сумма углов в треугольнике равна \(180^{\circ}\), тогда \(\angle ABC = 180^{\circ} - \angle A - \angle C = 180^{\circ} - 51^{\circ} - 77^{\circ} = 52^{\circ}\). Так как \(BD\) – биссектриса, то \(\angle CBD = 0,5\cdot \angle ABC = 26^{\circ}\).
Треугольники \(PBD\) и \(CBD\) равны по двум сторонам и углу между ними, тогда \(\angle PDB = \angle CDB\). \(\angle CDB = 180^{\circ} - \angle CBD - \angle C = 180^{\circ} - 26^{\circ} - 77^{\circ} = 77^{\circ}\), тогда \(\angle PDC = 2\cdot \angle CDB = 154^{\circ}\). Тогда \(\angle ADP = 180^{\circ} - 154^{\circ} = 26^{\circ}\).
Ответ: 26