Центральные и вписанные углы окружности (страница 3)

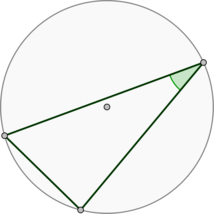
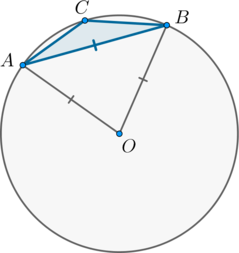
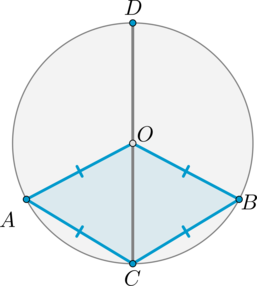
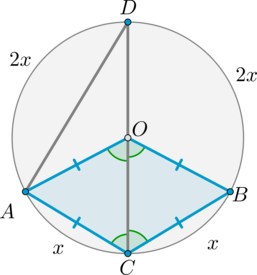
Обозначим хорду за \(AB\). Рассмотрим \(\triangle AOB\), где \(O\) – центр окружности.



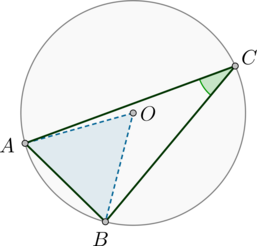
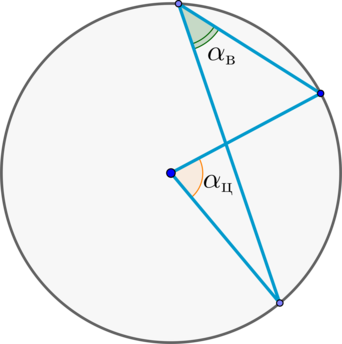
Так как \(AB\) равна радиусу окружности, то \(\triangle AOB\) – равносторонний. Следовательно, \(\angle AOB=60^\circ\). Заметим, что \(\angle AOB\) и \(\angle ACB\) – центральный и вписанный углы, опирающиеся на одну и ту же дугу, следовательно, \(\angle ACB=0,5\angle AOB=30^\circ\).

Ответ: 30

Построим отрезки \(CA\), \(AD\) и \(CB\), точку пересечения \(CD\) и \(AB\) обозначим \(E\).



\(\angle BCD = \angle BAD\) как вписанные, опирающиеся на общую дугу. Так как \(AB\) – диаметр, то \(\angle BCA = 90^{\circ}\).

Тогда \(\angle BCD\) дополняет \(\angle DCA\) до \(90^{\circ}\), а \(\angle BAD\) дополняет \(\angle CDA\) до \(90^{\circ}\) и из равенства \(\angle BCD = \angle BAD\) вытекает \(\angle DCA = \angle CDA\), следовательно, дуги \(AC\) и \(AD\) равны.

Ответ: 0

\(\triangle AOB\) равносторонний, следовательно, \(\angle AOB=\buildrel\smile\over{AB}=60^\circ\). Тогда большая дуга \(AB\) равна \(360^\circ-60^\circ=300^\circ\). Угол \(ACB\) – вписанный угол, опирающийся на большую дугу \(AB\), следовательно, равен ее половине: \(\angle ACB=\frac12\cdot 300^\circ=150^\circ.\)

Ответ: 150

Построим диаметр \(CF\). Пусть \(O\) – центр окружности, тогда \(\angle COA = 90^{\circ}\).



\(\angle CEA = 90^{\circ} - \angle DCF\).

Так как градусная мера дуги \(CBD\) равна \(150^{\circ}\), а \(CF\) – диаметр, то градусная мера дуги \(DF\) равна \(180^{\circ} - 150^{\circ} = 30^{\circ}\).

Вписанный угол в два раза меньше градусной меры дуги, на которую он опирается, тогда \(\angle DCF = 0,5\cdot 30^{\circ} = 15^{\circ}\), следовательно, \(\angle CEA = 90^{\circ} - 15^{\circ} = 75^{\circ}\).

Ответ: 75

Четырехугольник, все стороны которого равны, является ромбом. Следовательно, \(AOBC\) – ромб. Значит, диагонали делят его углы пополам. Следовательно, \(\angle AOC=\angle BOC=\angle ACO=\angle BCO=x\).

Следовательно, \(\buildrel\smile\over{AC}=\buildrel\smile\over{CB}=x\) (т.к. на них опираются центральные углы \(AOC\) и \(BOC\), равные этим дугам), \(\buildrel\smile\over{AD}=\buildrel\smile\over{DB}=2x\) (т.к. на них опираются вписанные углы \(ACD\) и \(BCD\), равные половинам этих дуг).

Т.к. вся окружность равна \(360^\circ\), то \(x+x+2x+2x=360^\circ \quad \Rightarrow \quad x=60^\circ\).

Угол \(ADC\) – вписанный и опирающийся на дугу \(\buildrel\smile\over{AC}\), следовательно, он равен ее половине, то есть \(30^\circ\).

Ответ: 30

Рассмотрим картинку:

Т.к. \(BC\parallel AD\), то \(\angle CBT=\angle DAT=30^\circ\). \(\angle DCK\), как вписанный и опирающийся на дугу \(KD\), равен ее половине, то есть \(20^\circ\). \(\angle CKD\) опирается на диаметр \(CD\), следовательно, равен половине от половины окружности, то есть \(90^\circ\). Значит, \(\angle CDK=180^\circ -90^\circ -20^\circ=70^\circ\).

\(\angle BTD\) — внешний угол для треугольника \(ATD\), следовательно, он равен сумме двух углов треугольника, не смежных с ним: \(\angle BTD=\angle TDA+\angle TAD=30^\circ+70^\circ=100^\circ\).

Ответ: 100

Рассмотрим картинку:

Т.к. \(\triangle BAC\) и \(DAC\) – равнобедренные, то \(\angle BAC=\angle BCA, \ \angle DAC=\angle DCA\). Таким образом, \(\angle A=\angle C\).

Т.к. \(\angle A, \angle C\) – вписанные, то \(\angle A+\angle C=\frac12\left(\buildrel\smile\over{DCB}+\buildrel\smile\over{DAB}\right)\).
Заметим, что эти дуги в сумме дают всю окружность, то есть \(360^\circ\). Следовательно, \(\angle A+\angle C=180^\circ\), следовательно, \(\angle A=\angle C=90^\circ\).

Ответ: 90