6. Геометрия на плоскости (планиметрия). Часть II
Окружность называется описанной около выпуклого многоугольника, если все вершины этого многоугольника лежат на окружности.
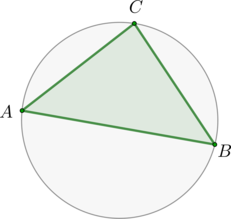
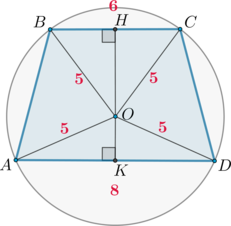
\(\blacktriangleright\) Около любого треугольника можно описать окружность. Ее центр лежит на пересечении серединных перпендикуляров к сторонам треугольника (рис. 1).
Для вписанного треугольника верна формула \[\dfrac{a}{\sin\alpha}=2R,\] где \(\alpha\) – угол треугольника, лежащий против стороны \(a\).
Площадь вписанного треугольника вычисляется по формуле
\[\Large{S_{\triangle}=\dfrac{abc}{4R}}\]
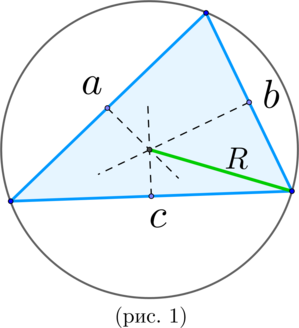
\(\blacktriangleright\) Если около выпуклого четырехугольника описана окружность, то сумма его противоположных углов равна \(\large{\angle\phi + \angle\gamma=180^\circ}\).
И наоборот: Если сумма двух противоположных углов выпуклого четырехугольника равна \(\large{\angle\phi +
\angle\gamma=180^\circ}\), то около него можно описать окружность. (рис. 2)
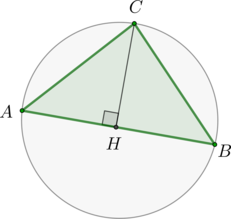
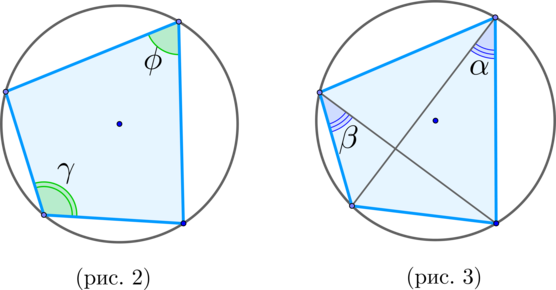
\(\blacktriangleright\) Около выпуклого четырехугольника описана окружность \(\Leftrightarrow\) \(\large{\angle \alpha =\angle
\beta}\). (рис. 3)
Площадь вписанного четырехугольника вычисляется по формуле
\[{\large{S_{\text{впис.4-к}}=\sqrt{(p-a)(p-b)(p-c)(p-d)},}}\]
где \(a,b,c,d\) – его стороны, \(p=\frac12(a+b+c+d)\) – полупериметр.
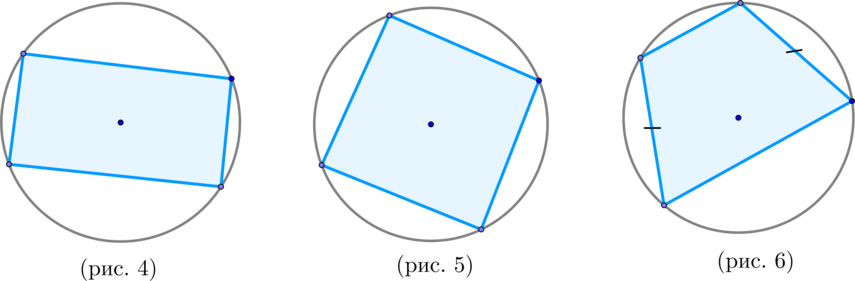
\(\blacktriangleright\) Если около параллелограмма описана окружность, то он – прямоугольник (рис. 4).
\(\blacktriangleright\) Если около ромба описана окружность, то он – квадрат (рис. 5).
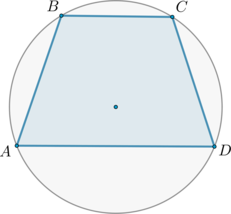
\(\blacktriangleright\) Если около трапеции описана окружность, то она равнобедренная.
И наоборот: около равнобедренной (и только равнобедренной) трапеции можно описать окружность (рис. 6).
Сторона \(AB\) треугольника \(ABC\) равна \(1\). Противолежащий ей угол \(C\) равен \(30^\circ\). Найдите радиус окружности, описанной около этого треугольника.
По теореме синусов \[\dfrac{AB}{\sin\angle C}=2R\] Следовательно, \[R=\dfrac12\cdot \dfrac{1}{\sin30^\circ}=\dfrac12\cdot \dfrac1{\frac12}=1\]
Ответ: 1
Одна сторона остроугольного треугольника равна радиусу описанной около него окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах.
Пусть \(AB=R\). Тогда нужно найти \(\angle C\). По теореме синусов: \[\dfrac{AB}{\sin \angle C}=2R\quad\Rightarrow\quad \sin\angle C=\dfrac{AB}{2R}=\dfrac R{2R}=\dfrac12\] Так как треугольник остроугольный, то \(\angle C=30^\circ\).
Ответ: 30
Угол \(C\) треугольника \(ABC\), вписанного в окружность радиуса \(3\), равен \(30^\circ\). Найдите сторону \(AB\) этого треугольника.
По теореме синусов \[\dfrac{AB}{\sin\angle C}=2R\] Следовательно, \[AB=2R\cdot \sin\angle C=2\cdot 3\cdot \sin30^\circ=3\]
Ответ: 3
Сторона \(AB\) треугольника \(ABC\) равна \(1\). Противолежащий ей угол \(C\) равен \(150^\circ\). Найдите радиус окружности, описанной около этого треугольника.
По теореме синусов \[\dfrac{AB}{\sin\angle C}=2R\] Следовательно, \[R=\dfrac12\cdot \dfrac{1}{\sin150^\circ}=\dfrac12\cdot \dfrac1{\frac12}=1\]
Ответ: 1
Сторона \(AB\) тупоугольного треугольника \(ABC\) равна радиусу описанной около него окружности. Найдите угол \(C\). Ответ дайте в градусах.
Пусть \(AB=R\). По теореме синусов: \[\dfrac{AB}{\sin \angle C}=2R\quad\Rightarrow\quad \sin\angle C=\dfrac{AB}{2R}=\dfrac R{2R}=\dfrac12\] Так как \(\angle C\) тупой, то \(\angle C=150^\circ\).
Ответ: 150
Боковые стороны равнобедренного треугольника равны \(40\), основание равно \(48\). Найдите радиус окружности, описанной около этого треугольника.
1 способ.
Пусть \(AC=BC\). Проведем \(CH\perp AB\).
Тогда \(CH\) также является и медианой, следовательно, \(AH=0,5AB=24\). Тогда \(\cos\angle
A=AH:AC=24:40=3:5\). Следовательно, \[\sin\angle
A=\sqrt{1-\cos^2\angle A}=\sqrt{1-\dfrac9{25}}=\dfrac45\] По теореме синусов \[\dfrac{BC}{\sin\angle A}=2R\quad\Rightarrow\quad
R=\dfrac12\cdot \dfrac{40}{\frac45}=25\]
2 способ.
Если \(R\) – радиус описанной окружности, то верна формула \[R=\dfrac{AB\cdot BC\cdot AC}{4S_{ABC}}\] Найдем площадь треугольника по формуле Герона (полупериметр \(p=64\)): \[S_{ABC}=\sqrt{64\cdot (64-40)(64-40)(64-48)}=8\cdot 24\cdot 4\] Тогда \[R=\dfrac{40\cdot 40\cdot 48}{4\cdot 8\cdot 24\cdot 4}=25\]
Ответ: 25
Основания равнобедренной трапеции равны \(8\) и \(6\). Радиус описанной окружности равен \(5\). Найдите высоту трапеции.
Пусть \(O\) – центр окружности. Проведем радиусы \(OA, OB, OC, OD\). Пусть \(OH\perp BC, OK\perp AD\).
Так как \(BC\parallel
AD\) и \(OH\perp BC, OK\perp AD\), то точки \(H, O, K\) лежат на одной прямой. Следовательно, \(HK\) – высота трапеции.
Рассмотрим \(\triangle BCO\). По формуле Герона его площадь равна \(S_{BOC}=\sqrt{8\cdot 2\cdot 3\cdot 3}=12\). С другой стороны, \(S_{BCO}=0,5BC\cdot OH\), откуда \[12=0,5BC\cdot OH\quad\Rightarrow\quad OH=4\] Рассмотрим \(\triangle ADO\). Аналогично ищем \(S_{ADO}=12\) и \(S_{ADO}=0,5AD\cdot OK\), откуда \(OK=3\). Следовательно, \(HK=4+3=7\).
Ответ: 7
