Окружность: важные теоремы, связанные с длинами отрезков (страница 2)

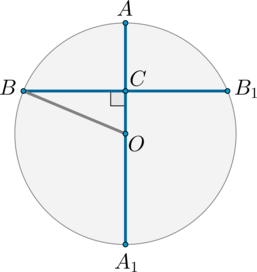
Рассмотрим картинку: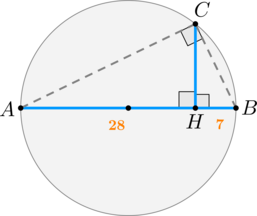

Т.к. угол \(ACB\) опирается на диаметр, то он прямой. Следовательно, треугольник \(ABC\) прямоугольный, и \(CH\) – высота, опущенная из вершины прямого угла. Следовательно, она делит треугольник \(ABC\) на два подобных треугольника \(ACH\) и \(BCH\). Значит:

\[\dfrac{AH}{CH}=\dfrac{CH}{HB} \quad \Rightarrow \quad CH^2=AH\cdot HB \quad \Rightarrow \quad CH=\sqrt{28\cdot 7}=14.\]

Ответ: 14

Докажем, что диаметр – это хорда наибольшей длины. Пусть \(MN\) – произвольная хорда, не являющаяся диаметром, а \(MK\) – диаметр. Тогда треугольник \(MNK\) прямоугольный, \(MK\) – гипотенуза, \(MN\) – катет, следовательно, \(MK > MN\), то есть диаметр больше любой хорды.



Чтобы радиус исходной окружности был наименьшим, необходимо, чтобы хорда \(AB\) была наибольшей, то есть чтобы \(AB\) была диаметром окружности. При этом \(AB = 2R > 1,5 R\), то есть условие выполнено.

Таким образом, наименьшее возможное значение \(R\) равно \(AB : 2 = 10 : 2 = 5\).

Ответ: 5

Отрезки касательных, проведённых из одной точки, равны: \(AB = AC\). Покажем это: Построим радиусы \(OB\) и \(OC\) и соединим \(OA\)

Так как радиус, проведённый в точку касания, перпендикулярен касательной, то \(\angle ACO = 90^{\circ} = \angle ABO\).
\(OC = OB\), как радиусы, тогда
в прямоугольных треугольниках \(AOC\) и \(AOB\) катеты \(OC\) и \(OB\) равны, а гипотенуза \(AO\) – общая, следовательно, треугольники \(AOC\) и \(AOB\) равны по катету и гипотенузе, откуда получаем \(AB = AC\).

Таким образом, треугольник \(ABC\) – равнобедренный и \[\angle ACB = \angle ABC = 0,5(180^{\circ} - \angle CAB) = 61^{\circ}.\]

Ответ: 61

Рассмотрим картинку:

Проведем из центра окружности точки \(O\) радиус \(OB\). Т.к. весь диаметр равен \(18+32=50\), то радиус равен \(25\). Следовательно, \(OB=25, \ OC=25-18=7\).

Т.к. радиус, перпендикулярный хорде, делит ее пополам, то \(BC=CB_1\). Найдем \(BC\). Треугольник \(BOC\) – прямоугольный, следовательно, \[BC^2=BO^2-OC^2 \quad \Rightarrow \quad BC^2=25^2-7^2=24^2 \quad \Rightarrow \quad BC=24\]

Значит, \(BB_1=2BC=48\).

Ответ: 48

Равные дуги стягивают равные хорды: \(DC = AB\). Покажем это:
Построим радиусы \(OC\) и \(OA\)

Так как дуги \(CD\) и \(AB\) равны, то их градусные меры совпадают, тогда \(\angle COD = \angle AOB\), как центральные углы, опирающиеся на равные дуги.
\(CO = OD = AO = OB\), как радиусы, тогда
треугольники \(AOB\) и \(DOC\) равны по двум сторонам и углу между ними, следовательно, \(DC = AB\).
\(QD = QC + CD = QA + AB\), тогда треугольник \(QBD\) – равнобедренный и \(63^{\circ} = \angle QBD = \angle QDB\), значит \[\angle BQD = 180^{\circ} - 63^{\circ} - 63^{\circ} = 54^{\circ}.\]

Ответ: 54

Рассмотрим картинку (пусть \(B, C\) – точки касания):

Т.к. отрезки касательных, проведенные из одной точки, равны, то \(MB=MX\) и \(NC=NX\). Т.к. радиусы, проведенные в точку касания, перпендикулярны касательной, то \(\angle OCN=\angle OXN=\angle OXM=\angle OBM=90^\circ\). Таким образом, по двум катетам равны треугольники: \(\triangle OBM=\triangle OXM\) и \(\triangle OXN=\triangle OCN\).
Значит, \(\angle BOM=\angle XOM\) и \(\angle XON=\angle CON\).

Следовательно, \(\angle MON=\frac12 \angle BOC\).

Т.к. в четырехугольнике сумма углов равна \(360^\circ\), то в четырехугольнике \(ABOC\): \[\angle BOC=360^\circ-90^\circ-90^\circ-\angle A=180^\circ-\angle A.\]

Следовательно, \[\angle MON=\dfrac12\left(180^\circ-\angle A\right)=90^\circ-\dfrac12\angle A=90^\circ-\dfrac12\cdot 32^\circ=74^\circ.\]

Ответ: 74

Рассмотрим картинку:

Т.к. отрезки касательных, проведенные из одной точки, равны, то \(AB=AC=10\), \(MB=MX\) и \(NC=NX\).

Следовательно, периметр

\(P_{\triangle AMN}=AM+MN+AN=AM+(MX+XN)+AN=\)

\(=AM+(MB+NC)+AN=(AM+MB)+(NC+AN)=AB+AC=10+10=20.\)

Ответ: 20