Окружность, вписанная в многоугольник или угол (страница 3)

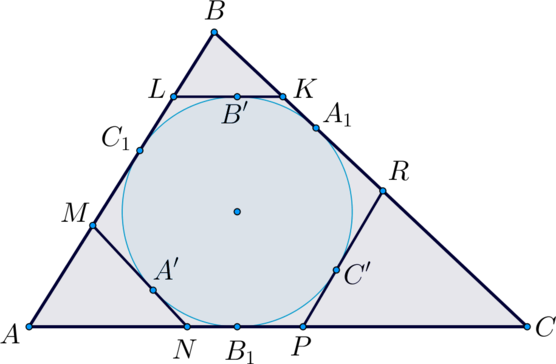
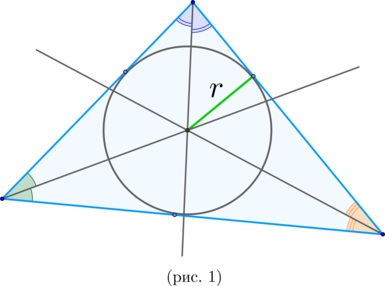
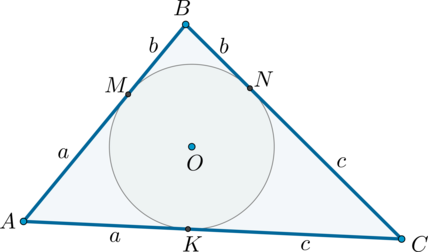
Рассмотрим рисунок. Пусть \(A_1, B_1, C_1\) – точки касания сторон \(\triangle ABC\) с окружностью. \(A', B', C'\) – точки на окружности, через которые проведены касательные параллельно сторонам треугольника. Получились треугольники \(AMN, BLK, CPR\). Пусть \(P_{AMN}=5, P_{BLK}=6, P_{CPR}=7\).
Так как отрезки касательных, проведенных из одной точки к окружности, равны, то \(MA'=MC_1, NA'=NB_1\). Следовательно, \[P_{AMN}=AM+MA'+NA'+AN=AM+MC_1+NB_1+AN=AC_1+AB_1=5\] Аналогично для других треугольников: \[\begin{aligned} &P_{BLK}=BC_1+BA_1=6\\ &P_{CPR}=CA_1+CB_1=7 \end{aligned}\] Следовательно, \[P_{ABC}=(AC_1+AB_1)+(BC_1+BA_1)+(CA_1+CB_1)=5+6+7=18.\]

Ответ: 18

Т.к. центр вписанной окружности лежит на пересечении биссектрис углов треугольника, то \(AO, BO, CO\) – биссектрисы углов \(A, B, C\) соответственно.



Следовательно, \(\angle A+\angle B+\angle C=2\angle BAO+2\angle ABO+2\angle BCO=180^\circ\), откуда \(\angle BCO=90^\circ -\angle BAO-\angle ABO=90^\circ-20^\circ-35^\circ=35^\circ\).

Ответ: 35

Рассмотрим рисунок:

Т.к. отрезки касательных, проведенных из одной точки, равны, то \(CN=CM\), \(BM=BK\), \(AN=AK\). Таким образом, периметр

\(P=AC+CB+BA=AC+CM+MB+BA=AC+CN+BK+BA=\)
\(=(AC+CN)+(KB+BA)=AN+KA=2AN\)

Следовательно, \(AN=\frac12P=10\).

Ответ: 10

Рассмотрим прямоугольный треугольник \(ABC\) (\(\angle C=90^\circ\)), \(AB=20\). Пусть \(O\) – центр вписанной в него окружности. Пусть также \(A_1, B_1, C_1\) – точки касания на сторонах \(BC, AC, AB\) соответственно.

Т.к. отрезки касательных, проведенных из одной точки к окружности, равны, то \[AC_1=AB_1=x; \qquad BC_1=BA_1=y; \qquad CA_1=CB_1.\]

Заметим также, что радиусы \(OB_1\) и \(OA_1\) перпендикулярны \(AC\) и \(BC\) соответственно (как радиусы, проведенные в точку касания). Следовательно, \(CB_1OA_1\) – прямоугольник (четырехугольник, имеющий три прямых угла). Но т.к. его смежные стороны равны, то это – квадрат. Следовательно, \(CA_1=CB_1=4\).

Тогда периметр треугольника равен:

\[AB+BC+CA=(x+y)+(y+4)+(4+x)=2(x+y)+4+4=2\cdot 20+8=48.\]

Ответ: 48

Пусть дан ромб \(ABCD\), \(AB=8\), \(O\) – центр окружности, вписанной в этот ромб. Т.к. центр окружности, вписанной в многоугольник, лежит на пересечении биссектрис его углов, то \(O\) – точка пересечения диагоналей ромба (т.к. они являются биссектрисами углов ромба). Пусть \(K\) – точка касания окружности со стороной \(AB\). Тогда \(OK=r\) – радиус окружности.

Рассмотрим треугольники \(OKA\) и \(OBA\). Они подобны по двум углам. Следовательно, \[\dfrac{OK}{OB}=\dfrac{OA}{AB} \quad \Rightarrow \quad r=OK=\dfrac{OA\cdot OB}{AB}\]

Т.к. площадь ромба равна полупроизведению диагоналей, то \(S=\frac12\cdot AC\cdot BD=\frac12\cdot 2\,OA\cdot 2\,OB=2\,OA\cdot OB=10\). Отсюда \(OA\cdot OB=5\). Следовательно,

\[r=\dfrac58=0,625.\]

Ответ: 0,625

1) Пусть в треугольнике \(BC=13\), \(AC-AB=5\). Таким образом, наибольшей стороной будет или \(AC\), или \(BC\).

Т.к. отрезки касательных, проведенных из одной точки к окружности, равны, то \(AM=AK=a\), \(BM=BN=b\), \(CN=CK=c\) (где \(M,N,K\) – точки касания).

Таким образом, из условия следует, что \(b+c=13\), \(a+c-(a+b)=c-b=5\). Решая систему из этих двух уравнений, находим, что \(b=4\), \(c=9\).

2) Заметим, что полупериметр данного треугольника равен \(a+b+c=a+13\), а площадь по формуле Герона равна
\(S=\sqrt{(a+b+c)(a+b+c-(a+b))(a+b+c-(a+c))(a+b+c-(b+c))}=\)

\(=\sqrt{(a+b+c)\cdot a\cdot b\cdot c}=6\sqrt{a(a+13)}.\)

Тогда по формуле (площадь равна полупериметру, умноженному на радиус вписанной окружности) имеем:

\[S=(a+b+c)\cdot r \quad \Rightarrow \quad 6\sqrt{a(a+13)}= (a+13)\cdot 2,4\sqrt3 \quad \Rightarrow \quad 36a=(a+13)\cdot \left(\dfrac{12}5\sqrt3\right)^2,\]

откуда \(a=12\). Следовательно, \(AC=12+9=21>BC\). Значит, большая сторона равна \(21\).

Ответ: 21

Обозначим точки касания окружности и сторон угла за \(A\) и \(C\). Тогда известно, что \(AC=3\sqrt3\). Пусть также \(O\) – центр окружности.

Тогда \(OA\) – радиус окружности, причем \(OA\perp BA\) (т.к. \(BA\) – касательная, а радиус, проведенный в точку касания, перпендикулярен касательной).

Рассмотрим \(\triangle ABC\): он равнобедренный (\(AB=BC\) как отрезки касательных, проведенных из одной точки), следовательно, \(\angle A=\angle C=0,5\cdot(180^\circ-60^\circ)=60^\circ\). Таким образом, он равносторонний, следовательно, \(AB=AC=3\sqrt3\).

Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть \(\angle ABO=30^\circ\). Тогда из прямоугольного \(\triangle ABO\):

\[\mathrm{tg}\,30^\circ=\dfrac{OA}{BA}=\dfrac{OA}{3\sqrt3} \quad \Rightarrow \quad OA=3\sqrt3\cdot \dfrac{\sqrt3}3=3.\]

Ответ: 3