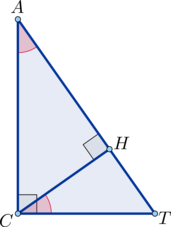
В треугольнике \(ABC\): высота \(CH\) равна \(2\sqrt6\), косинус угла \(A\) равен \(0,2\). Найдите \(AC\).
Рассмотрим \(\triangle ABC\):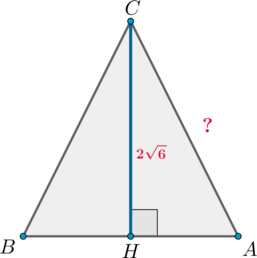
Так как косинус угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе, то в \(\triangle AHC:\) \[\cos A=\dfrac{AH}{AC}=\dfrac15\] Следовательно, можно принять \(AH=x\), \(AC=5x\). Тогда по теореме Пифагора из этого же треугольника: \[AC^2=AH^2+CH^2 \quad\Rightarrow\quad 25x^2=x^2+24 \quad\Leftrightarrow\quad x=\pm 1.\] Так как длина отрезка – неотрицательное число, то \(x=1\) и \(AC=5x=5.\)
Ответ: 5