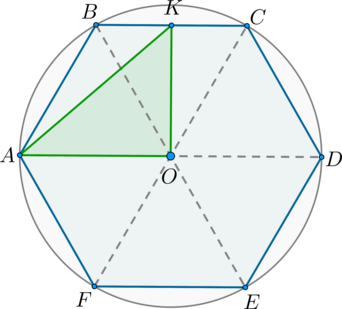
Сторона правильного шестиугольника \(ABCDEF\) равна \(\sqrt[4]{3}\). Найдите его площадь.
Пусть \(O\) – центр описанной около \(ABCDEF\) окружности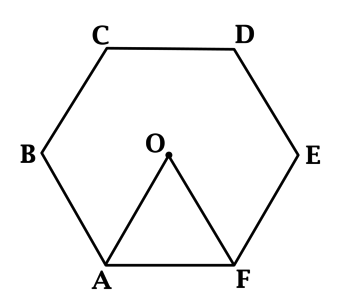
тогда треугольники \(AOF\), \(AOB\), \(BOC\), \(COD\), \(DOE\), \(EOF\) – равносторонние и все они попарно равны.
\[S_{\triangle{AOF}} = 0,5 AF^2 \cdot \sin{60^{\circ}} = \dfrac{AF^2\sqrt{3}}{4}, \qquad\qquad S_{ABCDEF} = 6\cdot S_{\triangle{AOF}} = \dfrac{3\sqrt{3}AF^2}{2}.\] В данной задаче \(S_{ABCDEF} = 6\cdot S_{\triangle{AOF}} = \dfrac{3\sqrt{3}AF^2}{2} = 4,5\).
Ответ: 4,5