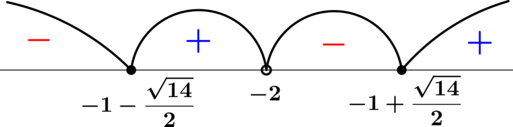Неравенства, решаемые методом рационализации (страница 3)

Рассмотрим первую скобку: \(\left(9^{x^2+x-2}-\left(3^{x+2}+1\right)\cdot 3^{x^2+x-2}+3^{x+2}\right)\).

Сделаем замену \(t=3^{x^2+x-2}\). Тогда данное выражение преобразуется к виду

\[t^2-\left(3^{x+2}+1\right)t+3^{x+2}=t^2-3^{x+2}t-t+3^{x+2}=t\left(t-3^{x+2}\right)- \left(t-3^{x+2}\right)=\left(t-3^{x+2}\right)\left(t-1\right)\]

Таким образом, данное выражение имеет вид:

\[\left(3^{x^2+x-2}-3^{x+2}\right)\left(3^{x^2+x-2}-1\right)\]

Тогда все неравенство примет вид:

\[\left(3^{x^2+x-2}-3^{x+2}\right)\left(3^{x^2+x-2}-1\right)\cdot \log_{x^2-3}{\left(3^{x^2+2x+2}-2\right)}\geqslant 0\]

1) Найдем ОДЗ левой части:

\[\begin{cases} x^2-3>0\\ x^2-3\ne 1\\[1ex] 3^{x^2+2x+2}-2>0 \end{cases} \quad \Rightarrow \quad \begin{cases} x\in(-\infty;-\sqrt3)\cup(\sqrt3;+\infty)\\ x\ne \pm 2\\ 3^{x^2+2x+2}>3^{\log_32} \end{cases} \quad \Rightarrow \quad \begin{cases} x\in(-\infty;-\sqrt3)\cup(\sqrt3;+\infty)\\ x\ne \pm 2\\ x^2+2x+2>\log_32 \end{cases}\]

Решим последнее неравенство отдельно:

\[x^2+2x+2>\log_32 \quad \Rightarrow \quad x^2+2x+1>\log_32-1 \quad \Rightarrow \quad (x+1)^2>\log_32-\log_33=\log_3{\frac23}\]

Заметим, что число \(\log_3{\frac23}<0\), следовательно, при любых \(x\) выражение \((x+1)^2\) будет больше отрицательного числа, то есть решением этого неравенства являются \(x\in \mathbb{R}\).

Таким образом, ОДЗ исходного неравенства: \(x\in (-\infty;-2)\cup(-2;-\sqrt3)\cup(\sqrt3;2)\cup(2;+\infty)\).

2) Перейдем к решению самого неравенства на ОДЗ.

Применим метод рационализации для первого множителя (скобки) и для второго множителя (логарифма):

\((x^2+x-2-0)(x^2+x-2-(x+2))\cdot (x^2-3-1)(3^{x^2+2x+2}-2-1)\geqslant 0\quad \Rightarrow\)

\(\Rightarrow \quad (x^2+x-2)(x^2-4)\cdot (x^2-4)(x^2+2x+2-1)\geqslant 0\quad \Rightarrow \)

\(\Rightarrow \quad (x-1)(x+2)(x+2)(x-2)\cdot (x-2)(x+2)(x+1)^2\geqslant 0 \quad \Rightarrow\)

\(\Rightarrow \quad (x-1)(x+2)^3(x-2)^2(x+1)^2\geqslant 0\)

Решим данное неравенство методом интервалов:

Таким образом, нам подходят точки \(x\in (-\infty;-2]\cup\{-1\}\cup[1;+\infty)\).

3) Пересечем полученный ответ с ОДЗ и получим:

\[x\in (-\infty;-2)\cup(\sqrt3;2)\cup(2;+\infty).\]

Ответ:

\(x\in (-\infty;-2)\cup(\sqrt3;2)\cup(2;+\infty)\)

ОДЗ:

\[\begin{cases} 2x^2+4x-4 > 0\\ x + 2 \neq 0\\ (-2x^2-4x + 4)^2 > 0 \end{cases} \qquad\Leftrightarrow\qquad x \in (-\infty; -1-\sqrt{3})\cup(-1+\sqrt{3}; +\infty).\]

Так как \((-a)^2 = a^2\), то \((-2x^2-4x+4)^2 = (2x^2+4x-4)^2\).
Обозначим \[A = 2x^2+4x-4,\] тогда \[\dfrac{(x^2+x)\lg A}{|x+2|}\geqslant\dfrac{\lg A^2}{x+2}\] Рассмотрим 2 случая:
1) \(x + 2 > 0\Rightarrow |x + 2| = x + 2\).
\[\dfrac{(x^2+x)\lg A - 2\lg A}{x+2} \geqslant 0 \qquad\Leftrightarrow\qquad \dfrac{(x^2+x-2)\lg A}{x+2} \geqslant 0.\] По методу рационализации это неравенство на ОДЗ равносильно:

\[\begin{aligned} &\dfrac{(x^2+x-2)(10-1)(A-1)}{x+2} \geqslant 0\quad\Leftrightarrow\quad \dfrac{(x^2+x-2)(2x^2+4x-5)}{x+2} \geqslant 0\\ &\Leftrightarrow\qquad \dfrac{(x - 1)(x + 2)\left(x + 1 + \dfrac{\sqrt{14}}{2}\right)\left(x + 1 - \dfrac{\sqrt{14}}{2}\right)}{x+2} \geqslant 0 \end{aligned}\]

По методу интервалов:



откуда \(x \in\left[-1 - \dfrac{\sqrt{14}}{2}; -2\right)\cup\left(-2; -1 + \dfrac{\sqrt{14}}{2}\right]\cup[1; +\infty)\).
Пересечем с условием \(x + 2 > 0\): \(x \in\left(-2; -1 + \dfrac{\sqrt{14}}{2}\right]\cup[1; +\infty)\)

2) \(x + 2 < 0\Rightarrow |x + 2| = -x - 2\).
\[\dfrac{-(x^2+x)\lg A - 2\lg A}{x+2} \geqslant 0\qquad\Leftrightarrow\qquad \dfrac{(x^2+x+2)\lg A}{x+2} \leqslant 0\] По методу рационализации это неравенство на ОДЗ равносильно:

\[\begin{aligned} &\dfrac{(x^2+x+2)(10-1)(A-1)}{x+2} \leqslant 0 \quad\Leftrightarrow\quad \dfrac{(x^2+x+2)(2x^2+4x-5)}{x+2} \leqslant 0\quad\Leftrightarrow\\ &\Leftrightarrow\quad \dfrac{(x^2+x+2)\left(x + 1 + \dfrac{\sqrt{14}}{2}\right)\left(x + 1 - \dfrac{\sqrt{14}}{2}\right)}{x+2} \leqslant 0 \end{aligned}\]

По методу интервалов:



откуда \(x \in\left(-\infty; -1-\dfrac{\sqrt{14}}{2}\right]\cup\left(-2; -1+\dfrac{\sqrt{14}}{2}\right]\).
Пересечем с условием \(x + 2 < 0\): \(x \in\left(-\infty; -1-\dfrac{\sqrt{14}}{2}\right]\).
Объединенное решение двух случаев: \(x\in\left(-\infty; -1-\dfrac{\sqrt{14}}{2}\right]\cup\left(-2; -1 + \dfrac{\sqrt{14}}{2}\right]\cup[1; +\infty)\).
Пересечем ответ с ОДЗ: \(x \in \left(-\infty; -1-\dfrac{\sqrt{14}}{2}\right]\cup\left(-1+\sqrt{3}; -1 + \dfrac{\sqrt{14}}{2}\right]\cup[1; +\infty)\).
Окончательный ответ \[x \in \left(-\infty; -1-\dfrac{\sqrt{14}}{2}\right]\cup\left(-1+\sqrt{3}; -1 + \dfrac{\sqrt{14}}{2}\right]\cup[1; +\infty)\,.\]

Ответ:

\(\left(-\infty; -1-\dfrac{\sqrt{14}}{2}\right]\cup\left(-1+\sqrt{3}; -1 + \dfrac{\sqrt{14}}{2}\right]\cup[1; +\infty)\)

ОДЗ: \[\begin{cases} x + 11 > 0\\ x + 11\neq 1\\ x^2 + 3 > 0\\ x > 0\\ x\neq 1\\ \sqrt{x + 11} > 0\\ \sqrt{x + 11} \neq 1\\ x^2 - 1 > 0\\ x^2 - 1\neq 1 \end{cases} \qquad\Leftrightarrow\qquad \begin{cases} x > 1\\ x\neq\sqrt{2} \end{cases}\]

На ОДЗ:
исходное неравенство равносильно неравенству

\[\begin{aligned} &\log_{(x + 11)} (x^2 + 3) \geqslant -\log_{\sqrt{x + 11}}x + \log_{(x + 11)}(x^2 - 1)\quad\Leftrightarrow\\ &\Leftrightarrow\quad\log_{(x + 11)} (x^2 + 3) - \log_{(x + 11)}(x^2 - 1) + \log_{\sqrt{x + 11}}x\geqslant 0\quad\Leftrightarrow\\ &\Leftrightarrow\quad \log_{(x + 11)} \dfrac{x^2 + 3}{x^2 - 1} + \log_{\sqrt{x + 11}}x\geqslant 0\quad\Leftrightarrow\quad \log_{(x + 11)} \dfrac{x^2 + 3}{x^2 - 1} + 2\log_{|x + 11|}x\geqslant 0\quad\Leftrightarrow\\ &\Leftrightarrow\quad\log_{(x + 11)} \dfrac{x^2 + 3}{x^2 - 1} + \log_{(x + 11)}x^2\geqslant 0\quad\Leftrightarrow\quad\log_{(x + 11)} \dfrac{x^2(x^2 + 3)}{x^2 - 1}\geqslant 0 \end{aligned}\]

По методу рационализации: на ОДЗ

\[\begin{aligned} &\log_{(x + 11)} \dfrac{x^2(x^2 + 3)}{x^2 - 1}\geqslant 0 \quad\Leftrightarrow\quad (x + 11 - 1)\left(\dfrac{x^2(x^2 + 3)}{x^2 - 1} - 1\right) \geqslant 0\quad\Leftrightarrow\\ &\Leftrightarrow\quad (x + 10)\cdot\dfrac{x^4 + 2x^2 + 1}{x^2 - 1} \geqslant 0\,. \end{aligned}\]

\[x^4 + 2x^2 + 1 = (x^2 + 1)^2 \geqslant 0,\] тогда

\[\begin{aligned} (x + 10)\cdot\dfrac{x^4 + 2x^2 + 1}{x^2 - 1} \geqslant 0\qquad\Leftrightarrow\qquad \left[ \begin{gathered} \dfrac{x + 10}{x^2 - 1} \geqslant 0\\ x^2 + 1 = 0 \end{gathered} \right. \end{aligned}\]

но на ОДЗ (при \(x > 1\), \(x\neq\sqrt{2}\)) у выражения \(\dfrac{x + 10}{x^2 - 1}\) числитель и знаменатель не обращаются в \(0\), тогда оно знакопостоянно при при \(x > 1\), \(x\neq\sqrt{2}\).

Так как \[\dfrac{x + 10}{x^2 - 1} > 0\qquad \text{при}\qquad x = 2,\] то у исходного неравенства множество решений совпадает с его ОДЗ.

Ответ:

\((1; \sqrt{2})\cup(\sqrt{2}; +\infty)\)

ОДЗ: \[\begin{cases} 1 + Nx > 0\\ 1 + Nx\neq 1 \qquad\text{— при любых}\ N\in\mathbb{N}\\ 1 + x > 0 \end{cases}\]

Покажем, что \(x < 0\) не подходят по ОДЗ:
зафиксируем произвольное \(x < 0\), тогда \(-x > 0\). Существует \(n\in\mathbb{N}\), такое что \[n > \dfrac{1}{-x}\,.\] Положим \(N = n\), тогда \[N > \dfrac{1}{-x}\qquad\Rightarrow\qquad -xN > 1\qquad\Rightarrow\qquad 1 + Nx < 0,\] что не подходит по ОДЗ. Таким образом, \(x\geqslant 0\).

Также по ОДЗ не подходит \(x = 0\), а \(x > 0\) подходят по ОДЗ, следовательно,
ОДЗ: \[x > 0\,.\] На ОДЗ:
исходное неравенство равносильно неравенству

\[\begin{aligned} &\dfrac{1}{\log_{3}(1 + Nx)}\cdot\log_3(1 + x)^N\geqslant 1 \end{aligned}\]

Так как на ОДЗ \[1 + Nx > 1,\] то \(\log_{3}(1 + Nx) > 0\), следовательно,

\[\begin{aligned} &\dfrac{1}{\log_{3}(1 + Nx)}\cdot\log_3(1 + x)^N\geqslant 1\quad\Leftrightarrow\quad\log_3(1 + x)^N\geqslant \log_{3}(1 + Nx)\quad\Leftrightarrow\\ &\Leftrightarrow\quad (1 + x)^N\geqslant (1 + Nx). \end{aligned}\]

Зафиксируем произвольный \(x > 0\).
Докажем по индукции, что данное неравенство выполнено для всех \(N\in\mathbb{N}\):

1) \(N = 1\): \[1 + x \geqslant 1 + x\] – верно.

2) Рассмотрим произвольное \(m\in\mathbb{N}\), такое что \((1 + x)^m\geqslant 1 + mx\), тогда \[(1 + x)^{m + 1} = (1 + x)\cdot(1 + x)^m\geqslant (1 + x)\cdot(1 + mx) = 1 + mx + x + mx^2\geqslant 1 + x(m + 1),\] таким образом, мы доказали, что рассматриваемый \(x\) подходит. Так как мы фиксировали произвольный \(x > 0\), то все \(x > 0\) являются решениями исходной задачи.

Ответ:

\((0; +\infty)\)

Найдем ОДЗ неравенства: \[\begin{aligned} &4-3\cdot 3^{^\frac1x}>0\quad\Leftrightarrow\quad 3^{^\frac1x}<\dfrac43 \quad\Leftrightarrow\\[2ex] &\Leftrightarrow\quad 3^{^\frac1x}<3^{\log_3\left(\frac43\right)} \quad\Leftrightarrow\quad \dfrac1x<\log_3\dfrac43\quad\Leftrightarrow\\[2ex] &\Leftrightarrow\quad \dfrac{1-x\cdot \log_3\frac43}x<0 \quad\Leftrightarrow\quad \dfrac{x-\log_{\frac43}3}x>0\quad\Leftrightarrow\\[2ex] &\Leftrightarrow\quad x\in (-\infty;0)\cup\left(\log_{\frac43}3;+\infty\right)\end{aligned}\] Решим неравенство на ОДЗ. Его можно преобразовать так: \[x\cdot \left(-\log_3\left(4-3\cdot 3^{^\frac1x}\right)-\dfrac1x\right)>0 \quad\Leftrightarrow\quad x\cdot \left(\log_3\left(4-3\cdot 3^{^\frac1x}\right)+\log_3 3^{^\frac1x}\right)<0\] Так как \(\log_ab+\log_ac=\log_a(bc)\), то \[x\cdot \log_3\left(4\cdot 3^{^\frac1x}-3\cdot \left(3^{^\frac1x}\right)^2\right)<0\] По методу рационализации на ОДЗ данное неравенство равносильно \[x\cdot (3-1)\cdot \left(4\cdot 3^{^\frac1x}-3\cdot \left(3^{^\frac1x}\right)^2-1\right)<0\quad\Leftrightarrow\quad x\cdot \left(4\cdot 3^{^\frac1x}-3\cdot \left(3^{^\frac1x}\right)^2-1\right)<0\] Найдем нули скобки. Сделаем замену \(3^{^\frac1x}=t\), тогда скобка примет вид \(4t-3t^2-1\). Чтобы найти ее нули, нужно решить уравнение \(4t-3t^2-1=0\). Его корни: \(t_1=1\), \(t_2=\frac13\). Следовательно, выражение \(4t-3t^2-1\) можно переписать в виде \(-3(t-1)\left(t-\frac13\right)\). Значит, наше неравенство примет вид \[x\cdot (-3)\cdot \left(3^{^\frac1x}-1\right)\cdot \left(3^{^\frac1x}-\dfrac13\right)<0\quad\Leftrightarrow\quad x\cdot \left(3^{^\frac1x}-3^0\right)\cdot \left(3^{^\frac1x}-3^{-1}\right)>0\] По методу рационализации данное неравенство преобразуется в неравенство \[x\cdot (3-1)\cdot \left(\dfrac1x-0\right)\cdot (3-1)\cdot \left(\dfrac1x-(-1)\right)>0\quad\Leftrightarrow\quad \dfrac{x(x+1)}{x^2}>0\] Решая полученное неравенство методом интервалов, получим ответ
\(x\in (-\infty;-1)\cup(0;+\infty)\).
Пересечем данный ответ с ОДЗ и получим итоговый ответ \[x\in (-\infty;-1)\cup\left(\log_{\frac43}3;+\infty\right)\]

Ответ:

\(x\in (-\infty;-1)\cup\left(\log_{\frac43}3;+\infty\right)\)

Выпишем ОДЗ неравенства: \[\begin{aligned} &\begin{cases} (x^2-6x-6)^2>0\\ 4+x-3x^2\ne 0\end{cases}\quad\Leftrightarrow\quad \begin{cases} x^2-6x-6\ne 0\\3x^2-x-4\ne 0\end{cases}\quad\Leftrightarrow\\ &\Leftrightarrow\quad x\ne -1; \ 3-\sqrt{15}; \ \dfrac43; \ 3+\sqrt{15}\end{aligned}\] Будем далее решать неравенство на ОДЗ (то есть как будто оно выполнено, а в конце решения полученный ответ пересечем с ОДЗ).

Предлагается сделать следующее: воспользоваться формулой \(\log_ab=\dfrac1{\log_ba}\), чтобы “перевернуть” логарифмы, тем самым у них станут одинаковые основания. НО! Данная формула верна только в том случае, когда \(b\ne 1\) (так как основание логарифма не может быть равно \(1\)).
Наше ОДЗ этого не учитывает. Следовательно, нужно рассмотреть два случая: когда “будущее” основание, то есть \((x^2-6x-6)^2\), равно \(1\), и когда не равно.

1) Пусть \((x^2-6x-6)^2=1\): \[\begin{aligned} &(x^2-6x-6)^2=1\quad\Leftrightarrow\quad x^2-6x-6=\pm 1\quad\Leftrightarrow\\[2ex] &\Leftrightarrow\quad x=-1; \ 3-\sqrt{14}; \ 3+\sqrt{14}; \ 7\end{aligned}\] Сразу исключим значение \(x=-1\), так как оно не входит в ОДЗ.
При остальных трех значениях \(x\) числитель дроби нашего неравенства будет равен: \[\log_51-\log_{11}1=0-0=0\] Следовательно, вне зависимости от того, чему будет равен знаменатель (главное, чтобы не был равен нулю), вся дробь будет равна нулю. Так как нам нужно, чтобы эта дробь была больше или равна нулю, то данные три значения \(x=3-\sqrt{14}; \ 3+\sqrt{14}; \ 7\) нам подходят.
Следовательно, их нужно будет включить в окончательный ответ.

2) Пусть \((x^2-6x-6)^2\ne 1\). Следовательно, \(x\ne 3-\sqrt{14}; \ 3+\sqrt{14}; \ 7\).
Тогда можно воспользоваться формулой \(\log_ab=\dfrac1{\log_ba}\): Можно применить метод рационализации для данного неравенства. Все множители вида \(\log_ab\) заменяются на \((a-1)(b-1)\); все множители вида \(\log_ab-\log_ac\) заменяются на \((a-1)(b-c)\): \[\begin{aligned} &\dfrac{((x^2-6x-6)^2-1)(11-5)} {(3x^2-x-4)((x^2-6x-6)^2-1)(5-1)((x^2-6x-6)^2-1)(11-1)}\leqslant 0\\[3ex] &\dfrac{(x^2-6x-6-1)(x^2-6x-6+1)}{(3x^2-x-4)(x^2-6x-6-1)^2(x^2-6x-6+1)^2}\leqslant 0\\[3ex] &\dfrac{(x+1)(x-7)(x-(3-\sqrt{14}))(x-(3+\sqrt{14}))} {(x+1)(3x-4)(x+1)^2(x-7)^2(x-(3-\sqrt{14}))^2(x-(3+\sqrt{14}))^2}\leqslant 0\end{aligned}\] Полученное неравенство можно решить методом интервалов:

Таким образом, ответ: \(x\in \left(3-\sqrt{14}; \frac43\right)\cup(3+\sqrt{14};7)\).

Теперь нужно объединить решения пунктов 1 и 2 и пересечь полученное множество с ОДЗ.
Получим окончательный ответ в неравенстве: \[x\in \left[3-\sqrt{14};\frac43\right)\cup [3+\sqrt{14};3+\sqrt{15})\cup(3+\sqrt{15};7]\]

Ответ:

\(\left[3-\sqrt{14};\frac43\right)\cup[3+\sqrt{14};3+\sqrt{15})\cup(3+\sqrt{15};7]\)