Решите неравенство
\[\begin{aligned} \dfrac{9^x - 3^{x + 1} - 19}{3^x - 6} + \dfrac{9^{x + 1} - 3^{x + 4} + 2}{3^x - 9}\leqslant 10\cdot 3^x + 3 \end{aligned}\]
(ЕГЭ 2016, резервный день)
Сделаем замену \(3^x = t > 0\):
\[\begin{aligned} \dfrac{t^2 - 3t - 19}{t - 6} + \dfrac{9t^2 - 81t + 2}{t - 9}\leqslant 10t + 3 \end{aligned}\]
ОДЗ:
\[\begin{aligned} \begin{cases} t\neq 6\\ t\neq 9 \end{cases} \end{aligned}\]
Перенесём всё влево и приведём к общему знаменателю
\[\begin{aligned} \dfrac{t - 3}{(t - 9)(t - 6)}\leqslant 0 \end{aligned}\]
По методу интервалов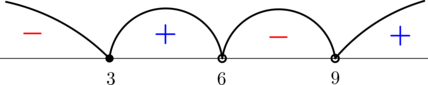
откуда \(t\in(-\infty; 3]\cup(6; 9)\)
с учётом ОДЗ и условия \(t > 0\): \(t\in(0; 3]\cup(6; 9)\)
в исходных переменных: \[x\in(-\infty; 1]\cup(\log_3 6; 2).\]
Ответ:
\((-\infty; 1]\cup(\log_3 6; 2)\)