Решите неравенство
\[\begin{aligned} \dfrac{(x - e)(x^2 - e)}{(2x - e)(x^2 + e)}\leqslant 0 \end{aligned}\]
ОДЗ: \[\begin{aligned} (2x - e)(x^2 + e)\neq 0 \end{aligned}\]
Решим полученное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.
1) Нули числителя находятся из уравнения \[(x - e)(x^2 - e) = 0\quad\Leftrightarrow\quad (x - e)(x - \sqrt{e})(x + \sqrt{e}) = 0\] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: \[x = e,\qquad\qquad x = \sqrt{e},\qquad\qquad x = -\sqrt{e}\]
2) Найдём нули знаменателя: \[(2x - e)(x^2 + e) = 0\] так как \(x^2\geqslant 0\), то \(x^2 + e\geqslant e > 0\), следовательно, знаменатель обращается в \(0\) только при \(x = \dfrac{e}{2}\).
Сравним \(\dfrac{e}{2}\) и \(\sqrt{e}\). Так как \(\dfrac{e}{2} > 0\) и \(\sqrt{e} > 0\), то \[\dfrac{e}{2}\ast \sqrt{e}\qquad\Leftrightarrow\qquad \dfrac{e^2}{4}\ast e\qquad\Leftrightarrow\qquad e\cdot \dfrac{e}{4}\ast e\cdot 1\qquad\Leftrightarrow\qquad \dfrac{e}{4}\ast 1\,,\] таким образом, \(\ast\) – это знак \(<\).
По методу интервалов:
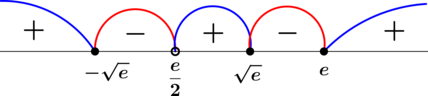
откуда \[x\in\left[-\sqrt{e}; \dfrac{e}{2}\right)\cup[\sqrt{e}; e]\,.\] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).
Ответ:
\(\left[-\sqrt{e}; \dfrac{e}{2}\right)\cup[\sqrt{e}; e]\)






