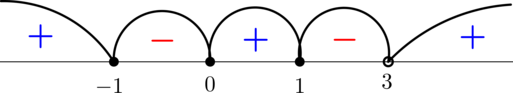Решение неравенств (страница 5)

Разложим на множители выражения \(2x^2+7x+6 \ \) и \( \ 2x^3+3x^2-8x-12\).
Решим сначала уравнение \[2x^2+7x+6=0 \quad \Rightarrow \quad x_1=-2\quad\text{и}\quad x_2=-\dfrac32.\] Тогда выражение можно переписать в виде \[2x^2+7x+6=2\left(x+\frac32\right)(x+2)=(2x+3)(x+2).\]

Решим уравнение \[2x^3+3x^2-8x-12=0\] Оно является кубическим. Т.к. остальные знаменатели содержат скобки \((x-2)\), \((x+2)\), \((2x+3)\), то попробуем найти корень этого уравнения среди чисел \(2, -2, -\frac32\). Для этого подставим каждое число в уравнение и проверим, обращается ли оно в верное тождество. \[\begin{aligned} &2\cdot2^3+3\cdot 2^2-8\cdot 2-12=0 \quad \Leftrightarrow \quad 0=0\\[2ex] &2\cdot (-2)^3+2\cdot (-2)^2-8\cdot (-2)-12=0 \quad \Leftrightarrow \quad 0=0\\[2ex] &2\cdot \left(-\frac32\right)^3+3\cdot \left(-\frac32\right)^2-8\cdot \left(-\frac32\right)-12=0 \quad \Leftrightarrow \quad 0=0 \end{aligned}\]

Таким образом, каждое из чисел \(2, -2, -\frac32\) является корнем уравнения \(2x^3+3x^2-8x-12=0\). А т.к. это уравнение может иметь максимум 3 корня, то это и есть все его корни, то есть выражение \[2x^3+3x^2-8x-12=2(x-2)(x+2)\left(x+\frac32\right)=(x-2)(x+2)(2x+3).\]

Таким образом, неравенство принимает вид:   \(\dfrac1{(x+2)(x-2)}+\dfrac4{(x+2)(2x+3)}\leqslant \dfrac1{2x+3}+ \dfrac4{(x-2)(x+2)(2x+3)} \quad \Rightarrow\)   \(\Rightarrow \quad \dfrac{-x^2+6x-5}{(x-2)(x+2)(2x+3)}\leqslant 0 \quad \Rightarrow \quad \dfrac{(x-1)(x-5)}{(x-2)(x+2)(2x+3)}\geqslant 0\)  

Решим полученное неравенство методом интервалов:

Следовательно, решением неравенства будут \(x\in \left(-2;-\frac32\right)\cup\left[1;2\right)\cup[5;+\infty)\).

Ответ:

\(\left(-2;-\frac32\right)\cup\left[1;2\right)\cup[5;+\infty)\)

ОДЗ:

\[\begin{aligned} x^3 + 5x - 42 \neq 0 \end{aligned}\]

Найдём нули числителя: \[x^5 + 4x^3 - 5x = 0\qquad\Leftrightarrow\qquad x(x^4 + 4x^2 - 5) = 0\] Решим уравнение \(x^4 + 4x^2 - 5 = 0\) при помощи замены \(x^2 = t\geqslant 0\): \[t^2 + 4t - 5 = 0\qquad\Leftrightarrow\qquad t = -2 \pm 3,\] откуда \(x^2 = 1\), следовательно, \(x = \pm 1\).

Найдём нули знаменателя: \[x^3 + 5x - 42 = 0\] Можно угадать корень \(x = 3\). Знание корня многочлена позволяет поделить его столбиком на \(x - x_0\), где \(x_0\) – его корень, тогда \[\begin{array}{rr|l} x^3+0x^2+5x-42&&\negthickspace\underline{\qquad x-3 \qquad}\\ \underline{x^3 - 3x^2} \phantom{000000000}&&\negthickspace \ x^2 + 3x + 14\\[-3pt] 3x^2 + 5x\,\phantom{0000}&&\\ \underline{3x^2 - 9x\,}\phantom{0000}&&\\[-3pt] 14x - 42 &&\\ \underline{14x - 42}&&\\[-3pt] 0&&\\ \end{array}\] Так как \[x^2 + 3x + 14 = (x + 1,5)^2 + 11,75 > 0\,,\] то полное разложение знаменателя на множители: \[x^3 + 5x - 42 = (x - 3)(x^2 + 3x + 14)\]

По методу интервалов



откуда ответ с учётом ОДЗ:\[x\in[-1; 0]\cup[1; 3)\,.\]

Ответ:

\([-1; 0]\cup[1; 3)\)

ОДЗ:

\[\begin{aligned} x^3 + 2ex^2 + 3x + 6e\neq 0 \end{aligned}\]

Найдём нули числителя: \[x^3 - 3\pi x^2 + 3\pi^2 x - \pi^3 = 0\qquad\Leftrightarrow\qquad (x - \pi)^3 = 0\qquad\Leftrightarrow\qquad x = \pi\]

Найдём нули знаменателя:

\[\begin{aligned} &x^3 + 2ex^2 + 3x + 6e = 0\qquad\Leftrightarrow\qquad x^2(x + 2e) + 3(x + 2e) = 0\qquad\Leftrightarrow\\ &\Leftrightarrow\qquad (x^2 + 3)(x + 2e) = 0\qquad\Leftrightarrow\qquad x = -2e\,. \end{aligned}\]

Так как при любом \(x\in\mathbb{R}\) выполнено \(x^2 + 3 > 0\), то исходное неравенство равносильно неравенству

\[\begin{aligned} \dfrac{(x - \pi)^3}{x + 2e} > 0 \end{aligned}\]

По методу интервалов



таким образом, с учётом ОДЗ ответ: \[x\in(-\infty; -2e)\cup(\pi; +\infty)\,.\]

Ответ:

\((-\infty; -2e)\cup(\pi; +\infty)\)

ОДЗ: \[x\neq \sqrt{2}.\] Преобразуем исходное неравенство:

\[\begin{aligned} &\dfrac{1}{(x-\sqrt{2})^2} + 3x^2 -2\sqrt{2}x + 2 + 2\bigl(-2x(\sqrt{2} + 1) + (\sqrt{2} + 1)^2\bigr)\leqslant 2\qquad\Leftrightarrow\\ \Leftrightarrow\qquad&\dfrac{1}{(x-\sqrt{2})^2} + (x^2 -2\sqrt{2}x + 2) + 2\bigl(x^2 - 2x(\sqrt{2} + 1) + (\sqrt{2} + 1)^2\bigr)\leqslant 2\qquad\Leftrightarrow\\ \Leftrightarrow\qquad&\dfrac{1}{(x-\sqrt{2})^2} + (x - \sqrt{2})^2 + 2\bigl(x - (\sqrt{2} + 1)\bigr)^2\leqslant 2. \end{aligned}\]

Покажем, что при любом \(x\neq \sqrt{2}\) выполнено \[\dfrac{1}{(x - \sqrt{2})^2} + (x - \sqrt{2})^2\geqslant 2,\] причём равенство достигается только при \(x = \pm 1 + \sqrt{2}\):

при \(x\neq \sqrt{2}\):

\[\begin{aligned} &\dfrac{1}{(x - \sqrt{2})^2} + (x - \sqrt{2})^2\geqslant 2 \qquad\Leftrightarrow\qquad 1 + (x - \sqrt{2})^4 - 2(x - \sqrt{2})^2\geqslant 0\qquad\Leftrightarrow\\ &\Leftrightarrow\qquad \bigl((x - \sqrt{2})^2\bigr)^2 - 2\cdot(x - \sqrt{2})^2 + 1\geqslant 0\qquad\Leftrightarrow\qquad ((x - \sqrt{2})^2 - 1)^2\geqslant 0, \end{aligned}\]

что верно при всех допустимых \(x\). Равенство имеет место только при \((x - \sqrt{2})^2 = 1\) (это легко проверить аналогичным способом).

Таким образом, при всех \(x\neq \sqrt{2}\) выполнено \[\dfrac{1}{(x - \sqrt{2})^2} + (x - \sqrt{2})^2\geqslant 2,\] причём равенство достигается только при \((x - \sqrt{2})^2 = 1\), то есть при \(x = \pm 1 + \sqrt{2}\).

Так как при любом \(x\) выполнено \(2\bigl(x - (\sqrt{2} + 1)\bigr)^2\geqslant 0\), то с учётом доказанного утверждения неравенство

\[\begin{aligned} \dfrac{1}{(x-\sqrt{2})^2} + (x - \sqrt{2})^2 + 2\bigl(x - (\sqrt{2} + 1)\bigr)^2\leqslant 2 \end{aligned}\]

может выполняться только при \(x = \pm 1 + \sqrt{2}\).
При \(x = 1\) имеем:

\[\begin{aligned} \dfrac{1}{1} + 1 + 0\leqslant 2 \end{aligned}\]

– верно.
При \(x = -1\) имеем:

\[\begin{aligned} \dfrac{1}{1} + 1 + 8\leqslant 2 \end{aligned}\]

– неверно.

В итоге, ответ: \[x = 1 + \sqrt{2}.\]

Ответ:

\(1 + \sqrt{2}\)

ОДЗ:

\[\begin{aligned} \begin{cases} x\neq -C\\ x^2 + D\neq 0 \end{cases} \end{aligned}\]

Умножая исходное неравенство на \(-1\), получим равносильное неравенство

\[\begin{aligned} \dfrac{(x + A)(x - B)}{(x + C)(x^2 + D)}\leqslant 0 \end{aligned}\]

Покажем, что, например, подходит неравенство

\[\begin{aligned} \dfrac{(x + 1)(x - (-1))}{(x + 2)(x^2 + 0)}\leqslant 0\qquad\Leftrightarrow\qquad\dfrac{(x + 1)^2}{x^2(x + 2)}\leqslant 0 \end{aligned}\]

Решим полученное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.

1) Нули числителя находятся из уравнения \[(x + 1)^2 = (x + 1)(x + 1) = 0\] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: \[x = -1\]

2) Найдём нули знаменателя: \[x^2(x + 2) = 0\qquad\Leftrightarrow\qquad \left[ \begin{gathered} x = -2\\ x = 0 \end{gathered} \right.\]

По методу интервалов:



откуда и получаем требуемый ответ \[x\in(-\infty; -2)\cup\{-1\}\,.\] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).

Ответ:

\(A = 1,\, B = -1,\, C = 2,\, D = 0\)

ОДЗ:

\[\begin{aligned} \begin{cases} x\neq -1\\ x^2 - e\neq 0 \end{cases} \end{aligned}\]

Покажем, что в качестве искомой функции подходит \(f(x) = -(x - 1)(x + 1)(x^2 - e)(x + 2)\):

исходное неравенство примет вид

\[\begin{aligned} -\dfrac{(x - 1)(x - 1)(x + 1)(x^2 - e)(x + 2)}{(x + 1)(x^2 - e)} > 0\quad\Leftrightarrow\quad\dfrac{(x - 1)^2(x + 1)(x^2 - e)(x + 2)}{(x + 1)(x^2 - e)} < 0 \end{aligned}\]

Последнее неравенство на ОДЗ равносильно неравенству

\[\begin{aligned} \dfrac{(x - 1)^2(x + 2)}{1} < 0 \end{aligned}\]

Решим полученное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.

1) Нули числителя находятся из уравнения \[(x - 1)^2(x + 2) = 0\] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: \[x = 1,\qquad\qquad x = -2\]

2) Знаменатель нигде не обращается в \(0\).

По методу интервалов:



откуда \(x\in(-\infty; -2)\,.\) Пересекая полученный ответ с ОДЗ, получим требуемое: \[x\in(-\infty; -2)\,.\]

Ответ:

\(f(x) = -(x - 1)(x + 1)(x^2 - e)(x + 2)\)

ОДЗ: \[\begin{cases} x - 4\neq 0\\ x - 4^2\neq 0\\ \dots\\ x - 4^{1008}\neq 0 \end{cases}\] Так как \(2^{2k} = 4^k\), то на ОДЗ исходное неравенство равносильно неравенству

\[\begin{aligned} (x - 2)(x - 2^3)(x - 2^5)\cdot...\cdot(x - 2^{2015})\leqslant 0 \label{Res} \end{aligned}\]

Заметим, что количество скобок, участвующих в произведении – чётно (в произведении участвуют скобки вида \((x - 2^{2n - 1})\), где \(n\) пробегает всевозможные натуральные значения от \(1\) до \(1008\), то есть, скобок \(1008\)).

Решим последнее неравенство на ОДЗ методом интервалов. Для этого найдём нули левой части.

\[\begin{aligned} (x - 2)(x - 2^3)\cdot...\cdot(x - 2^{2015}) = 0 \end{aligned}\]

Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули левой части: \[x = 2,\qquad x = 2^3,\qquad ..,\qquad x = 2^{2015}.\]

По методу интервалов:



Здесь знаки чередуются.

При \(x > 2^{2016}\) выражение  положительно, тогда при учёте чётности количества скобок и того, что кратность каждого корня в произведении равна \(1\), получаем, что при \(x < 2\) выражение  также положительно, откуда \[x\in [2; 2^2)\cup(2^2; 2^3]\cup[2^5; 2^6)\cup(2^6; 2^7]\cup ...\cup [2^{2013}; 2^{2014})\cup(2^{2014}; 2^{2015}].\] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).

Ответ:

\([2; 2^2)\cup(2^2; 2^3]\cup[2^5; 2^6)\cup(2^6; 2^7]\cup ...\cup [2^{2013}; 2^{2014})\cup(2^{2014}; 2^{2015}]\)