Решение показательных неравенств (страница 7)

ОДЗ: \(x\) – произвольный.

Так как левая и правая части исходного неравенства положительны, то от них можно взять \(\log_2\), в результате чего получим равносильное неравенство

\[\begin{aligned} &3^{2x} + 2^x\cdot 3^x + 1 > \log_2 3^{\left(4^x - 2^x\cdot 3^{x + 1} + \log_3 2\right)}\qquad\Leftrightarrow\\ \Leftrightarrow\qquad &3^{2x} + 2^x\cdot 3^x + 1 > (4^x - 2^x\cdot 3^{x + 1} + \log_3 2)\cdot \log_2 3\qquad\Leftrightarrow\\ \Leftrightarrow\qquad &3^{2x} + 2^x\cdot 3^x + 1 > (4^x - 2^x\cdot 3^{x + 1})\cdot \log_2 3 + 1\qquad\Leftrightarrow\\ \Leftrightarrow\qquad &3^{2x} + 2^x\cdot 3^x > (4^x - 2^x\cdot 3^{x + 1})\cdot \log_2 3 \end{aligned}\]

Поделим последнее неравенство на \(2^x\cdot 3^x\):

\[\begin{aligned} \left(\dfrac{3}{2}\right)^{x} + 1 > \left(\left(\dfrac{2}{3}\right)^{x} - 3\right)\cdot \log_2 3 \end{aligned}\]

Сделаем замену \(\left(\dfrac{3}{2}\right)^x = t > 0\):

\[\begin{aligned} t + 1 > \left(\dfrac{1}{t} - 3\right)\cdot \log_2 3, \end{aligned}\]

что при \(t > 0\) равносильно

\[\begin{aligned} t^2 + t > \left(1 - 3t\right)\cdot \log_2 3\qquad\Leftrightarrow\qquad t^2 + (3\log_2 3 + 1)t - \log_2 3 > 0 \end{aligned}\]

Решим уравнение

\[\begin{aligned} t^2 + (3\log_2 3 + 1)t - \log_2 3 = 0 \end{aligned}\]

его дискриминант \(D = (3\log_2 3 + 1)^2 + 4\log_2 3 = 9(\log_2 3)^2 + 10\log_2 3 + 1, > 0,\) следовательно, \[t = \dfrac{-(3\log_2 3 + 1)\pm \sqrt{9(\log_2 3)^2 + 10\log_2 3 + 1}}{2},\] так как \(\log_2 3 > 0\), то \(D > (3\log_2 3 + 1)^2\), следовательно, ровно один из корней больше нуля:\[t = \dfrac{-(3\log_2 3 + 1) + \sqrt{9(\log_2 3)^2 + 10\log_2 3 + 1}}{2}\]

По методу интервалов при \(t > 0\)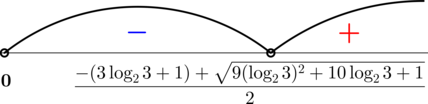



откуда \(t\in\left(\dfrac{-(3\log_2 3 + 1) + \sqrt{9(\log_2 3)^2 + 10\log_2 3 + 1}}{2}; +\infty\right)\), следовательно, \[x\in\left(\log_{\frac{3}{2}}\dfrac{-(3\log_2 3 + 1) + \sqrt{9(\log_2 3)^2 + 10\log_2 3 + 1}}{2}; +\infty\right)\,.\]

Ответ:

\(\left(\log_{\frac{3}{2}}\dfrac{-(3\log_2 3 + 1) + \sqrt{9(\log_2 3)^2 + 10\log_2 3 + 1}}{2}; +\infty\right)\)

Так как \(e^y > 0\) – при любых \(y\), то у уравнения \(x = e^{\frac{1}{x}}\) не может быть неположительных решений, следовательно, \(x_0 > 0\), следовательно, \[\ln x_0 = \dfrac{1}{x_0}.\]

ОДЗ исходного неравенства: \[x > 0.\] На ОДЗ \(x^x = e^{\ln x^x} = e^{x\ln x}\), тогда на ОДЗ исходное неравенство равносильно неравенству \[e^{x\ln x}\geqslant e^1\qquad\Leftrightarrow\qquad x\ln x\geqslant 1\qquad\Leftrightarrow\qquad \ln x\geqslant \dfrac{1}{x}.\]

На ОДЗ:
функция \(f(x) = \ln x\) – возрастает,   функция \(g(x) = \dfrac{1}{x}\) – убывает,   следовательно, на ОДЗ у уравнения \[f(x) = g(x)\qquad\Leftrightarrow\qquad\ln x = \dfrac{1}{x}\] не более одного корня. Заметим, что ОДЗ уравнения \(\ln x = \dfrac{1}{x}\) совпадает с ОДЗ исходного неравенства, следовательно, на ОДЗ \[f(x) = g(x)\qquad\Leftrightarrow\qquad x = x_0.\]

Так как на промежутке \((0; +\infty)\) \(f(x)\) – возрастает, а \(g(x)\) – убывает, то при \(x\in(0; x_0)\) выполнено \[f(x) < g(x),\] а при \(x\in[x_0; +\infty)\) выполнено \[f(x) \geqslant g(x)\,.\]

Таким образом, \(\ln x\geqslant \dfrac{1}{x}\) только при \(x\geqslant x_0\).

Ответ:

\([x_0; +\infty)\)

ОДЗ неравенства: \(x\in \mathbb{R}\).

Заметим, что \(x^2+x-30=(x-5)(x+6)\). Далее, так как \(3=7^{\log_73}\), то неравенство можно переписать в виде: \[{\large{7^{\,x-5}>\left(7^{\log_73}\right)^{(x-5)(x+6)} \quad\Leftrightarrow \quad 7^{(x-5)(x+6)\log_73}<7^{\,x-5}}}\] Так как показательная функция всегда положительная, то можно без последствий разделить обе части неравенства на \(7^{x-5}\): \[{\large{7^{(x-5)(x+6)\log_73-(x-5)}<1 \quad\Leftrightarrow\quad (x-5)(x+6)\log_73-(x-5)<0 \quad\Leftrightarrow\quad (x-5)((x+6)\log_73-1)<0}}\]

Решим данное неравенство методом интервалов. Корнями левой части являются \(x=5\) и \(x=\dfrac1{\log_73}-6=\log_37-6\). Так как \(1<\log_37<2\), то \(-5<\log_37-6<-4\).

Следовательно, \(x\in (\log_37-6;5)\).

Ответ:

\(x\in (\log_37-6;5)\)