Выпишем ОДЗ: \[\begin{cases} \sin x+\cos x+4>0\\
\sin x+\cos x+4\ne 1\\
x^2+1>0\\
2\sin x\cos x+4,5>0\\
2\sin x\cos x+4,5\ne 1 \end{cases}\] Так как по формуле вспомогательного аргумента \[\sin x+\cos
x=\sqrt2\left(\dfrac{\sqrt2}2\sin x+\dfrac{\sqrt2}2\cos
x\right)=\sqrt2\sin \left(x+\dfrac{\pi}4\right),\] а по формуле двойного угла \(2\sin x\cos x=\sin2x\), то \[\begin{cases}
\sin \left(x+\dfrac{\pi}4\right)>-2\sqrt2\\[2ex]
\sin \left(x+\dfrac{\pi}4\right) \ne -\dfrac32\sqrt2\\[2ex]
\sin 2x>-4,5\\
\sin 2x\ne -3,5 \end{cases} \quad\Leftrightarrow\quad x\in
\mathbb{R}.\]
Заметим, что при одинаковых аргументах один логарифм будет \(\geqslant \) другого логарифма в одном из двух случаев:
1) Аргументы этих логарифмов равны \(1\). Тогда \(x^2+1=1 \quad\Rightarrow\quad x=0\).
Тогда неравенство принимает вид: что на ОДЗ равносильно \[0\geqslant 0 \ ,\] что является верным неравенством. Следовательно, \(x=0\) является решением неравенства.
2) При \(x\ne 0\).
Заметим, что функция \(f(x)=\log_xa\) является убывающей (докажите это самостоятельно) при \(a>1\) и возрастающей при \(a<1\). В нашем случае \(x^2+1>1\), следовательно, функция убывает. Значит, чем больше значение функции, тем меньше значение \(x\). Следовательно, при \(x\ne
0\) неравенство равносильно \[\begin{aligned}
&\sin x+\cos x+4\leqslant 2\sin x\cos x+4,5
\quad\Leftrightarrow\\
&\Leftrightarrow\quad (1-2\cos x)\left(\sin
x-\dfrac12\right)\leqslant 0 \quad\Leftrightarrow\\
&\Leftrightarrow\quad \left(\cos x-\dfrac12\right)\left(\sin
x-\dfrac12\right)\geqslant 0
\end{aligned}\] Данное неравенство равносильно совокупности систем: \[\left[ \begin{gathered} \begin{aligned}
&\begin{cases}
\sin x\geqslant \dfrac12\\[2ex]
\cos x\geqslant \dfrac12
\end{cases}\\
&\begin{cases}
\sin x\leqslant \dfrac12\\[2ex]
\cos x\leqslant \dfrac12
\end{cases}
\end{aligned}\end{gathered}\right.\]
Решим каждую систему по окружности:
первая система:
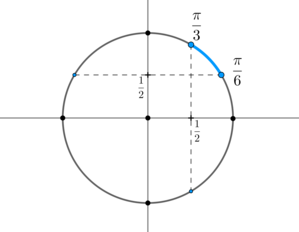
вторая система:
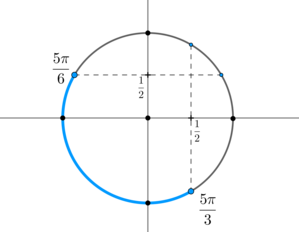
Тогда ответом будут \(x\in \left[\dfrac{\pi}6+2\pi
n;\dfrac{\pi}3+2\pi n\right]\cup \left[\dfrac{5\pi}6+2\pi n;
\dfrac{5\pi}3+2\pi n\right]\), \(n\in\mathbb{Z}\).
Тогда окончательный ответ – это объединение решений \(x=0\) и \(x\in
\left[\dfrac{\pi}6+2\pi n;\dfrac{\pi}3+2\pi n\right]\cup
\left[\dfrac{5\pi}6+2\pi n; \dfrac{5\pi}3+2\pi n\right]\), \(n\in\mathbb{Z}\), то есть \[x\in\left[\dfrac{\pi}6+2\pi
n;\dfrac{\pi}3+2\pi n\right]\cup \left[\dfrac{5\pi}6+2\pi n;
\dfrac{5\pi}3+2\pi n\right]\cup \{0\}, \quad n\in\mathbb{Z}.\]
Ответ:
\(x\in\left[\frac{\pi}6+2\pi n;\frac{\pi}3+2\pi n\right]\cup
\left[\frac{5\pi}6+2\pi n; \frac{5\pi}3+2\pi n\right]\cup \{0\},
\quad n\in\mathbb{Z}\)





