Решение сложных уравнений (страница 4)

а) ОДЗ: \(x\) – произвольное. Решим на ОДЗ.

Применим формулу суммы синусов: \(\sin\alpha+\sin \beta=2\sin \dfrac{\alpha+\beta}2\cos \dfrac{\alpha-\beta}2\) и получим:

\[2\sin 2x\cos x+\cos x=0 \Rightarrow \cos x\,(2\sin 2x+1)=0 \Rightarrow \left[ \begin{gathered}\begin{aligned} &\cos x=0\\ &\sin 2x=-\dfrac12 \end{aligned} \end{gathered}\right. \Rightarrow \left[ \begin{gathered}\begin{aligned} &x_1=\dfrac{\pi}2+\pi n, n\in\mathbb{Z}\\ &x_2=-\dfrac{\pi}{12}+\pi m, m\in\mathbb{Z}\\ &x_3=-\dfrac{5\pi}{12}+\pi k, k\in\mathbb{Z} \end{aligned} \end{gathered}\right.\]

б) Отберем корни по окружности: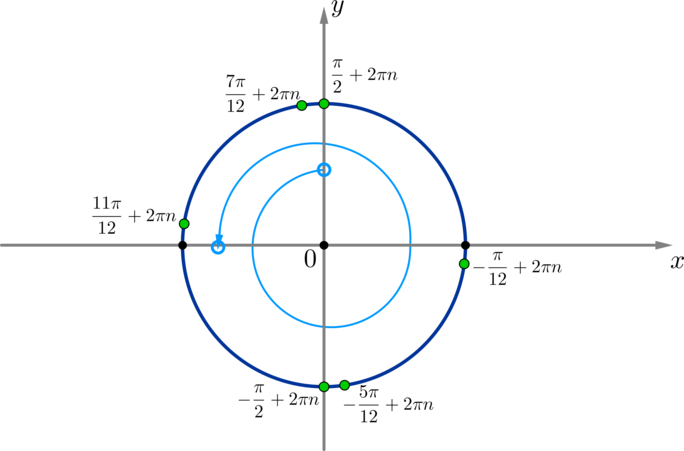

Отметим дугу, соответствующую промежутку \(\left(-\dfrac{3\pi}2;\pi\right)\): она отмечена голубым цветом (причем концы дуги выколоты). Таким образом, мы по одному разу проходимся по \(I, III, IV\) четвертям и два раза по \(II\) четверти.

Углы, попадающие на эту дугу:

\[\dfrac{7\pi}{12}-2\pi; \ \dfrac{11\pi}{12}-2\pi; \ -\dfrac{\pi}2; \ -\dfrac{5\pi}{12}; \ -\dfrac{\pi}{12}; \ \dfrac{\pi}2; \ \dfrac{7\pi}{12}; \ \dfrac{11\pi}{12}\]

Ответ:

а) \(\dfrac{\pi}2+\pi n, -\dfrac{\pi}{12}+\pi m, -\dfrac{5\pi}{12}+\pi k, \ n,m,k\in\mathbb{Z}\)

б) \(-\dfrac{17\pi}{12}; \ -\dfrac{13\pi}{12}; \ -\dfrac{\pi}2; \ -\dfrac{5\pi}{12}; \ -\dfrac{\pi}{12}; \ \dfrac{\pi}2; \ \dfrac{7\pi}{12}; \ \dfrac{11\pi}{12}\)

а) ОДЗ: \(\cos x\ne 0\). Решим на ОДЗ.

\[2\cos 3x+2\cos x=0 \Rightarrow \text{по формуле тройного угла для косинуса: } 2(4\cos^3x-3\cos x)+2\cos x=0 \Rightarrow\]

\[\cos x(8\cos^2x-4)=0 \Rightarrow \left[ \begin{gathered}\begin{aligned} &\cos x=0\\ &\cos^2x=\dfrac12 \end{aligned} \end{gathered}\right. \Rightarrow\]

Т.к. по ОДЗ \(\cos x\ne 0 \Rightarrow \) решением будет только \(\cos^2x=\dfrac12 \Rightarrow \cos x=\pm \dfrac{\sqrt2}2 \Rightarrow x=\dfrac{\pi}4+\dfrac{\pi}2n, n\in\mathbb{Z}\)

б) Отберем корни:

\(0<\dfrac{\pi}4+\dfrac{\pi}2n<3 \Rightarrow -\dfrac12<n<-\dfrac12+\dfrac6{\pi} \Rightarrow n=0;1 \Rightarrow x=\dfrac{\pi}4; \dfrac{3\pi}4\)

Ответ:

а) \(\dfrac{\pi}4+\dfrac{\pi}2n, n\in\mathbb{Z}\)

б) \(\dfrac{\pi}4; \dfrac{3\pi}4\)

а) Представим \(\sin 3x=\sin(5x-2x)=\sin 5x\cos 2x-\sin 2x\cos 5x\), тогда уравнение перепишется в виде: \[\sin 5x\cdot \cos 2x=\sin 5x\cdot \cos 2x-\sin 2x\cdot \cos 5x \quad\Leftrightarrow\quad \sin 2x\cdot \cos 5x=0 \quad\Leftrightarrow\] \[\Leftrightarrow\quad \left[ \begin{gathered}\begin{aligned} &2x=\pi n, n\in\mathbb{Z}\\[1ex] & 5x=\dfrac{\pi}2+\pi m, m\in\mathbb{Z} \end{aligned} \end{gathered}\right. \quad\Leftrightarrow\quad \left[ \begin{gathered}\begin{aligned} & x=\dfrac{\pi}2 n, n\in\mathbb{Z}\\[1ex] & x=\dfrac{\pi}{10}+\dfrac{\pi}5 m, m\in\mathbb{Z} \end{aligned} \end{gathered}\right.\]

б) Отберем корни.   \(\begin{aligned} & 2014\pi \leqslant \dfrac{\pi}2n\leqslant 2015\pi \quad\Leftrightarrow\quad 4028\leqslant n\leqslant 4030 \quad\Rightarrow\quad n=4028; \ 4029; \ 4030 \quad\Rightarrow\\[2ex] &\Rightarrow\quad x=2014\pi; \ 2014,5\pi; \ 2015\pi.\\[2ex] & 2014\pi\leqslant \dfrac{\pi}{10}+\dfrac{\pi}5m\leqslant 2015\pi \quad\Leftrightarrow\quad 10069,5\leqslant m\leqslant 10074,5 \quad\Rightarrow\\[2ex] &\Rightarrow\quad m=10070; \ 10071; \ 10072; \ 10073; \ 10074 \quad\Rightarrow\\[2ex] &\Rightarrow\quad x=2014,1\pi; \ 2014,3\pi; \ 2014,5\pi; \ 2014,7\pi; \ 2014,9\pi. \end{aligned}\)

Ответ:

а) \(\dfrac{\pi}2 n; \ \dfrac{\pi}{10}+\dfrac{\pi}5 m, n,m\in\mathbb{Z}\)  

б) \(2014\pi; \ 2014,5\pi; \ 2015\pi; \ 2014,1\pi; \ 2014,3\pi; \ 2014,5\pi; \ 2014,7\pi; \ 2014,9\pi\)

ОДЗ: \(x\) – произвольное. Решим на ОДЗ:

а) Исходное уравнение можно переписать в виде

\[2^n\sin^{2n}x\cdot\cos^n x\cdot 2^m\sin^{2m}(2x)\cdot\cos^{2m} (2x) = 1,\]

что равносильно

\[(2\sin x\cdot\cos x)^n\cdot\sin^n x\cdot (2\sin (2x)\cdot\cos (2x))^m\sin^{m}(2x)\cdot\cos^{m} (2x) = 1,\]

что равносильно

\[\sin^n (2x)\cdot\sin^n x\cdot \sin^m (4x)\cdot\sin^{m}(2x)\cdot\cos^{m} (2x) = 1.\]

Так как в произведении в левой части стоят \(2n + 3m\) множителей, модули которых не больше \(1\), а правая часть равна \(1\), то модули каждого из множителей в левой части должны быть равны \(1\) (иначе модуль левой части будет меньше 1, а модуль правой равен 1 и равенство невозможно).

Заметим, однако, что \(|\sin x|\) и \(|\sin 2x|\) не могут одновременно быть равны 1, так как если \(|\sin x| = 1\), то из основного тригонометрического тождества следует, что \(\cos x = 0\), тогда \(|\sin 2x| = |2\sin x\cdot\cos x| = 0\). Отсюда следует, что у данного уравнения нет решений ни при каких \(n, m\in\mathbb{N}\).

Ответ:

а) \(\varnothing\)

б) \(\varnothing\)