Разложение на множители тригонометрических уравнений (страница 2)

а) ОДЗ: \(x\) – произвольное. Решим на ОДЗ.

Перенесем все слагаемые в левую часть и вынесем общие множители за скобки:

\(2\cos2x(\sin x+1) -\sqrt3(\sin x+1)=0 \Rightarrow (\sin x+1)(2\cos 2x-\sqrt3)=0 \Rightarrow\)

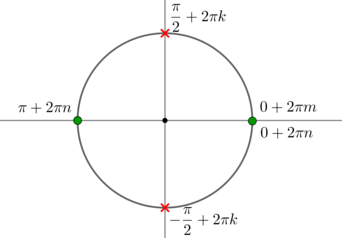
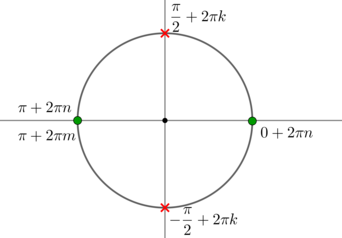
\(\left[ \begin{gathered}\begin{aligned} &\sin x=-1\\ &\cos 2x=\dfrac{\sqrt3}2 \end{aligned} \end{gathered}\right. \quad \Rightarrow\quad \left[ \begin{gathered}\begin{aligned} &x_1=-\dfrac{\pi}2+2\pi n, n\in\mathbb{Z}\\ &x_2=\dfrac{\pi}{12}+\pi m, m\in\mathbb{Z}\\ &x_3=-\dfrac{\pi}{12}+\pi k, k\in\mathbb{Z} \end{aligned} \end{gathered}\right. \)

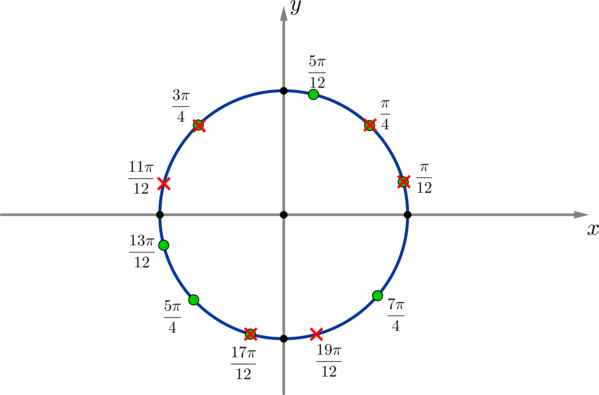
б) Отберем корни:

1) \(-\dfrac{\pi}2\leqslant x_1<\dfrac{3\pi}2 \Rightarrow 0\leqslant n<1 \Rightarrow n=0 \Rightarrow x=-\dfrac{\pi}2\)

2) \(-\dfrac{\pi}2\leqslant x_2<\dfrac{3\pi}2 \Rightarrow -\dfrac7{12}\leqslant m<\dfrac{17}{12} \Rightarrow m=0;1 \Rightarrow x=\dfrac{\pi}{12}; \dfrac{13\pi}{12}\)

3) \(-\dfrac{\pi}2\leqslant x_3<\dfrac{3\pi}2 \Rightarrow -\dfrac5{12}\leqslant k<\dfrac{19}{12} \Rightarrow k=0;1 \Rightarrow x=-\dfrac{\pi}{12}; \dfrac{11\pi}{12}\)

Ответ:

а) \(-\dfrac{\pi}2+2\pi n, \dfrac{\pi}{12}+\pi m, -\dfrac{\pi}{12}+\pi k, \ n,m,k\in\mathbb{Z}\)

б) \(-\dfrac{\pi}2; -\dfrac{\pi}{12};\dfrac{\pi}{12};\dfrac{11\pi}{12}\dfrac{13\pi}{12}\)

Заметим, что \(\dfrac{9\pi}8=\pi+\dfrac{\pi}8\), следовательно, сделаем замену \(x+\dfrac{\pi}8=t\):

\[\sin t=\sin(\pi+t) \quad\Leftrightarrow\quad \sin t=-\sin t \quad\Leftrightarrow\quad \sin t=0 \quad\Leftrightarrow\quad t=\pi n, n\in\mathbb{Z}\]

Тогда, вернувшись к изначальной переменной, получим ответ \[x=-\dfrac{\pi}8+\pi n, n\in\mathbb{Z}.\]

б) Отберем корни.

\(-\dfrac{3\pi}4\leqslant -\dfrac{\pi}8+\pi n\leqslant \dfrac{3\pi}4 \quad\Leftrightarrow\quad -\dfrac58\leqslant n\leqslant \dfrac78 \quad\Rightarrow\quad n=0.\) Следовательно, \(x=-\dfrac{\pi}8.\)

Ответ:

а) \(-\dfrac{\pi}8+\pi n, n\in\mathbb{Z}\)  

б) \(-\dfrac{\pi}8\)

а) Преобразуем уравнение: \[1+\sin2x=\sin^22x-2\sin2x\cos2x+\cos^22x \quad\Leftrightarrow\quad 1+\sin 2x=1-2\sin2x\cos2x \quad\Leftrightarrow\quad \sin2x(1+2\cos2x)=0\] Данное уравнение имеет решение в том случае, если либо \(\sin2x=0\), либо \(\cos2x=-\frac12\). В первом случае получаем серию корней \(2x=\pi n\), а во втором \(2x=\pm \frac{2\pi}3+2\pi m, \quad n,m\in\mathbb{Z}\), откуда: \[x=\dfrac{\pi}2n \quad {\small{\text{или}}} \quad x=\pm \dfrac{\pi}3+\pi m, \quad n,m\in\mathbb{Z}\]

б) Отберем корни.

\(\dfrac{\pi}2n >0\quad\Leftrightarrow\quad n>0\quad\Rightarrow\quad n_{min}=1 \quad\Rightarrow\quad x_{min}=\dfrac{\pi}2\)

\(\dfrac{\pi}3+\pi m>0\quad\Leftrightarrow\quad m>-\dfrac13\quad\Rightarrow\quad m_{min}=0 \quad\Rightarrow\quad x_{min}=\dfrac{\pi}3\)

\(-\dfrac{\pi}3+\pi m>0\quad\Leftrightarrow\quad m>\dfrac13\quad\Rightarrow\quad m_{min}=1\quad\Rightarrow\quad x_{min}=\dfrac{2\pi}3\)

Заметим, что среди найденных в каждой серии наименьших положительных корней самым меньшим является \(\dfrac{\pi}3\).

Ответ:

а) \(\dfrac{\pi}2n; \ \pm \dfrac{\pi}3+\pi m, \quad n,m\in\mathbb{Z}\)

б) \(\dfrac{\pi}3\)

а) Так как \(\mathrm{tg}\,x=\dfrac{\sin x}{\cos x}\) и \(\sin 2x=2\sin x\cos x\), то уравнение можно переписать в виде  

\(\sin x+\dfrac{\sin x}{\cos x}-\dfrac{2\sin x\cos x}{\cos x}=0 \quad\Leftrightarrow\quad \dfrac{\sin x\cos x+\sin x-2\sin x\cos x}{\cos x}=0\quad\Leftrightarrow\quad \dfrac{\sin x(1-\cos x)}{\cos x}=0 \quad\Leftrightarrow\)  

\(\Leftrightarrow \quad \begin{cases} \left[\begin{gathered}\begin{aligned} &\sin x=0\\ &\cos x=1 \end{aligned}\end{gathered}\right.\\ \cos x\ne 0\end{cases} \quad\Leftrightarrow\quad \begin{cases} \left[\begin{gathered}\begin{aligned} &x=\pi n, n\in\mathbb{Z}\\ &x=2\pi m, m\in\mathbb{Z} \end{aligned}\end{gathered}\right.\\[3ex] x\ne \dfrac{\pi}2+\pi k, k\in\mathbb{Z}\end{cases}\)   Для того, чтобы получить окончательный ответ, отметим решение на окружности:

Видим, что серия \(x=2\pi m\) входит в серию \(x=\pi n\). Следовательно, окончательный ответ \[x=\pi n, n\in\mathbb{Z}.\]

б) Отберем корни.

\(-\dfrac{\pi}2<\pi n<\dfrac{\pi}2\quad\Leftrightarrow\quad -\dfrac12<n<\dfrac12 \quad\Rightarrow\quad n=0.\) Следовательно, \(x=0\).

Ответ:

а) \(x=\pi n, n\in\mathbb{Z}\)

б) \(0\)

а) Так как \(\mathrm{tg}\,2x=\dfrac{\sin 2x}{\cos 2x}\), то уравнение, сделав замену \(2x=t\), можно переписать в виде  

\(\dfrac{\sin t}{\cos t}+\sin t=0 \quad\Leftrightarrow\quad \dfrac{\sin t+\sin t\cos t}{\cos t}=0\quad\Leftrightarrow\quad \dfrac{\sin t\cdot (1+\cos t)}{\cos t}=0 \quad\Leftrightarrow\)  

\(\Leftrightarrow \quad \begin{cases} \left[\begin{gathered}\begin{aligned} &\sin t=0\\ &\cos t=-1 \end{aligned}\end{gathered}\right.\\ \cos t\ne 0\end{cases} \quad\Leftrightarrow\quad \begin{cases} \left[\begin{gathered}\begin{aligned} &t=\pi n, n\in\mathbb{Z}\\ &t=\pi+2\pi m, m\in\mathbb{Z} \end{aligned}\end{gathered}\right.\\[3ex] t\ne \dfrac{\pi}2+\pi k, k\in\mathbb{Z}\end{cases}\)   Для того, чтобы получить окончательный ответ, отметим решение для \(t\) на окружности:

Видим, что серия \(t=\pi+2\pi m\) входит в серию \(t=\pi n\). Следовательно, окончательный ответ \[t=\pi n \quad\Rightarrow\quad x=\dfrac{\pi}2\cdot n, n\in\mathbb{Z}.\]

б) Отберем корни.

\(-3\pi\leqslant \dfrac{\pi}2\cdot n<-2\pi \quad\Leftrightarrow\quad -6\leqslant n<-4 \quad\Rightarrow\quad n=-6; \ -5.\) Следовательно, \(x=-3\pi; \ -\dfrac{5\pi}2.\)

Ответ:

а) \(\dfrac{\pi}2n, n\in\mathbb{Z}\)

б) \(-3\pi; \ -\dfrac{5\pi}2\)

а) ОДЗ: \(\sin 3x\ne \dfrac{\sqrt2}2\). Решим на ОДЗ.

На ОДЗ данное уравнение равносильно уравнению:

\[2\cos^2x-1-\sin4x=0 \Rightarrow \cos2x-\sin4x=0 \ \text{(т.к. по формуле двойного угла } \cos2x=2\cos^2x-1)\]

\[\cos2x-2\sin2x\cos2x=0 \Rightarrow \cos2x(1-2\sin2x)=0 \Rightarrow \left[ \begin{gathered}\begin{aligned} &\cos2x=0\\ &\sin2x=\dfrac12 \end{aligned} \end{gathered}\right. \Rightarrow \left[ \begin{gathered}\begin{aligned} &x=\dfrac{\pi}4+\dfrac{\pi}2n , n\in\mathbb{Z}\\ &x=\dfrac{\pi}{12}+\pi m, m\in\mathbb{Z}\\ &x=\dfrac{5\pi}{12}+\pi k, k\in\mathbb{Z} \end{aligned} \end{gathered}\right.\]

Решим ОДЗ: \(\sin 3x\ne \dfrac{\sqrt2}2 \Rightarrow x'\ne \dfrac{\pi}{12}+\dfrac23\pi p, p\in\mathbb{Z}, \ x''\ne \dfrac{\pi}4+\dfrac23\pi l, l\in\mathbb{Z}\)

Пересечем полученные корни с ОДЗ. Для этого отметим все эти точки на окружности: корни уравнения — зеленые, а корни ОДЗ – красными.

Таким образом, итоговый ответ: \[\begin{aligned} &x_1=\dfrac{5\pi}{12}+2\pi n, n\in\mathbb{Z}\\ &x_2=\dfrac{13\pi}{12}+2\pi m, m\in\mathbb{Z}\\ &x_2=\dfrac{5\pi}4+2\pi k, k\in\mathbb{Z}\\ &x_4=\dfrac{7\pi}4+2\pi l, l\in\mathbb{Z} \end{aligned}\]

б) Отберем корни:

1) \(\dfrac{19\pi}4\leqslant x_1\leqslant \dfrac{23\pi}4 \Rightarrow \dfrac{13}6\leqslant n \leqslant \dfrac83 \Rightarrow n\in\varnothing\)

2) \(\dfrac{19\pi}4\leqslant x_2\leqslant \dfrac{23\pi}4\Rightarrow \dfrac{11}6\leqslant m \leqslant \dfrac{7}3 \Rightarrow m=2 \Rightarrow x=\dfrac{61\pi}{12}\)

3) \(\dfrac{19\pi}4\leqslant x_3\leqslant \dfrac{23\pi}4 \Rightarrow \dfrac74\leqslant k\leqslant \dfrac94 \Rightarrow k=2 \Rightarrow x=\dfrac{21\pi}4\)

4) \(\dfrac{19\pi}4\leqslant x_4\leqslant \dfrac{23\pi}4 \Rightarrow \dfrac32\leqslant l\leqslant 2 \Rightarrow l=2 \Rightarrow x=\dfrac{23\pi}4\)

Ответ:

а) \(\dfrac{5\pi}{12}+2\pi n, \dfrac{13\pi}{12}+2\pi m, \dfrac{5\pi}4+2\pi k, \dfrac{7\pi}4+2\pi l, \ n,m,k,l\in\mathbb{Z}\)

б) \(\dfrac{61\pi}{12};\dfrac{21\pi}4;\dfrac{23\pi}4\)

ОДЗ: \(x\) – произвольное. Решим на ОДЗ:

а) Воспользуемся формулами для косинуса двойного угла и синуса двойного угла: \[\begin{aligned} &2\sin{x}\cdot \cos{x} + 2\cos^2{x} - 1 + 1 = 0.\\ &2\cos{x}\cdot (\sin{x} + \cos{x}) = 0. \end{aligned}\] Произведение выражений равно нулю тогда и только тогда, когда хотя бы одно из них равно нулю и все они не теряют смысла, следовательно, или \(\cos{x} = 0\), или \(\sin{x} + \cos{x} = 0\).

В случае \(\cos{x} = 0\):
решениями будут \(x = \dfrac{\pi}{2} +\pi k\), где \(k\in\mathbb{Z}\).

В случае \(\sin{x} + \cos{x} = 0\):
равенство можно разделить на \(\cos{x}\) (так как если \(\cos{x} = 0\) является решением, то из этого равенства следует, что и \(\sin x=0\); но тогда мы получаем противоречие с основным тригонометрическим тождеством: \(0^2+0^2=1\)).

После деления имеем: \(\mathrm{tg}\, x = -1\), откуда получаем \(x = -\dfrac{\pi}{4} +\pi k\), где \(k\in\mathbb{Z}\) – подходят по ОДЗ.

б) \[0 < \dfrac{\pi}{2} + \pi k < \pi\qquad\Leftrightarrow\qquad -\dfrac{\pi}{2} < \pi k < \dfrac{\pi}{2}\qquad\Leftrightarrow\qquad -\dfrac{1}{2} < k < \dfrac{1}{2},\] но \(k\in\mathbb{Z}\), тогда на интервал \((0; \pi)\) попадает только корень при \(k = 0\): \(x = \dfrac{\pi}{2}\).

\[0 < -\dfrac{\pi}{4} +\pi k < \pi\qquad\Leftrightarrow\qquad \dfrac{\pi}{4} < \pi k < \pi + \dfrac{\pi}{4}\qquad\Leftrightarrow\qquad \dfrac{1}{4} < k < 1\dfrac{1}{4},\] но \(k\in\mathbb{Z}\), тогда на интервал \((0; \pi)\) попадает только корень при \(k = 1\): \(x = \dfrac{3\pi}{4}\).

Ответ:

а) \(\dfrac{\pi}{2} + \pi k\), \(-\dfrac{\pi}{4} + \pi k\), где \(k\in\mathbb{Z}\)

б) \(\dfrac{\pi}{2}\), \(\dfrac{3\pi}{4}\)