Сложные задачи прикладного характера из ЕГЭ прошлых лет (страница 3)

Если фонд продаст акции в конце \(t\)-ого год, то на конец 25-ого года они пролежат в банке \(25-t\) лет. Так как каждый год банк увеличивает сумму в \(r\) раз, то за \(25-t\) лет он увеличит ее в \(r^{25-t}\) раз. Следовательно, на конец 25-ого года фонд будет иметь \[f(t)=t^2\cdot r^{25-t} \quad {\small{\text{тыс. рублей.}}}\]

Рассмотрим эту функцию. В ней \(r\) – некоторое конкретное, но неизвестное число, а \(t\) – переменная. Найдем ее производную: \[f'=2t\cdot r^{25-t}+t^2\cdot r^{25-t}\cdot \ln r\cdot (-1)=r^{25-t}\cdot t\cdot (2-t\ln r)\] Таким образом, нулем производной, учитывая, что \(t\geqslant 1\), является \(t=\dfrac2{\ln r}\).
Причем заметим, что эта точка является точкой максимума. Следовательно, до \(t=\frac2{\ln r}\) функция возрастает, а после – убывает.

Таким образом, если, продав акции в 21-ый год, фонд получит наибольшую из возможных прибыль, то это значит, что мы имеем такую картинку:

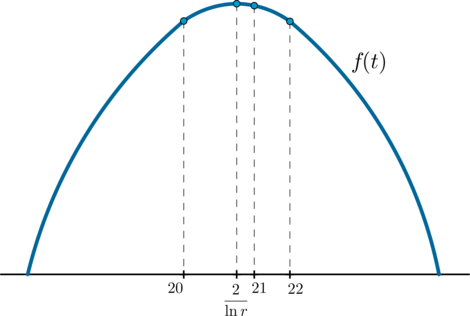
(Для примера на картинке точка \(t=21\) находится правее точки максимума, но левее \(t=22\); может быть наоборот: \(21\) будет находиться левее точки максимума, но правее \(20\). Главное, что \(21\) находится между \(20\) и \(22\) и ближе, чем \(20\) или \(22\), к точке максимума!)

То есть \(f(21)>f(20)\) и \(f(21)>f(22)\). Из этого условия будет следовать, что \(f(21)>f(t)\) при любом целом \(t\) от 1 до 25. Решим полученную систему: \[\begin{cases} 21^2\cdot r^4>20^2\cdot r^5\\ 21^2\cdot r^4>22^2\cdot r^3 \end{cases} \quad\Rightarrow\quad \begin{cases} r<\dfrac{21^2}{20^2}\\[2ex] r>\dfrac{22^2}{21^2} \end{cases}\] откуда получаем, что \(r\in\left(\dfrac{484}{441};\dfrac{441}{400}\right).\)

Ответ:

\(\left(\dfrac{484}{441};\dfrac{441}{400}\right)\)

Составим таблицу:

\[\begin{array}{|l|c|c|} \hline \text{Год}&\text{Размер вклада до}&\text{Размер вклада после}\\ &\text{начисления} \ \%&\text{начисления} \ \%\\ \hline 1&10&1,1\cdot 10\\ \hline 2&1,1\cdot 10&1,1^2\cdot 10\\ \hline 3&1,1^2\cdot 10+m&1,1(1,1^2\cdot 10+m)\\ \hline 4&1,1(1,1^2\cdot 10+m)+m&1,1(1,1(1,1^2\cdot 10+m)+m)\\ \hline \end{array}\]

Таким образом, в конце \(4\)-ого года размер вклада составит \(1,1(1,1(1,1^2\cdot 10+m)+m)\) млн рублей. Фраза “банк за \(4\) года начислит на вклад более \(7\) млн рублей” означает, что на конец \(4\)-ого года чистая прибыль по вкладу составит более \(7\) млн рублей.

Для того, чтобы вычислить чистую прибыль, нужно от всей суммы, которая находится на счете на конец \(4\)-ого года, отнять сумму, которую клиент вложил в банк. Таким образом, чистая прибыль составит:
\(1,1(1,1(1,1^2\cdot 10+m)+m)-(10+m+m)\)
Значит, получаем неравенство:
\(1,1(1,1(1,1^2\cdot 10+m)+m)-(10+m+m)>7 \Leftrightarrow 1,1^4\cdot 10+1,1^2m+1,1m-10-2m>7\)

Решив данное неравенство, получим: \(m>\dfrac{2359}{310} \Rightarrow\) наименьшее целое \(m=8\) млн рублей.

Ответ:

\(8\) млн рублей.

Составим таблицу, где \(\dfrac{100+r}{100}=t.\)

\(\begin{array}{|l|c|c|c|c|} \hline \text{Месяц} & \text{Долг в млн руб.} & \text{Долг в млн руб.} & \text{Долг в млн руб.} & \text{Выплата в млн руб.}\\ & \text{до начисления} & \text{после начисления} & \text{после выплаты} & \\ & \text{процентов} & \text{процентов} & & \\ \hline 1&1 &t &0,9 & t-0,9\\ \hline 2&0,9 &0,9t &0,8 & 0,9t-0,8\\ \hline 3&0,8 &0,8t &0,7 & 0,8t-0,7\\ \hline 4&0,7 &0,7t &0,6 & 0,7t-0,6\\ \hline 5&0,6 &0,6t &0,5 & 0,6t-0,5\\ \hline 6&0,5 &0,5t &0 & 0,5t\\ \hline \end{array}\)

Тогда общая сумма выплат составляет:
\(0,1t\cdot (10+9+8+7+6+5)-0,1(9+8+7+6+5)=4,5t-3,5\)
Т.к. общая сумма выплат должна быть более 1,3 млн, то имеем неравенство:
\(4,5t-3,5>1,3 \Leftrightarrow t>\dfrac{16}{15}\)

Таким образом, \(r>\dfrac{100}{15}\)
Т.к. \(r\) – целое, то наименьшее \(r\), удовлетворяющее неравенству — это \(r=7\).

Ответ:

\(7\%\).

Составим таблицу, обозначив за \(x\) млн рублей – годовой платеж в \(2020\) и \(2021\) годах.

\(\begin{array}{|l|c|c|c|} \hline \text{Год}&\text{Долг в августе }&\text{Долг в январе (после начисления процентов)}&\text{Платеж}\\ \hline 1&5,3 &(1+0,01y)\cdot 5,3 &0,01y\cdot 5,3\\ \hline 2&5,3 &(1+0,01y)\cdot 5,3 &0,01y\cdot 5,3\\ \hline 3&5,3 &(1+0,01y)\cdot 5,3 &0,01y\cdot 5,3\\ \hline 4&5,3 &(1+0,01y)\cdot 5,3 &x\\ \hline 5&(1+0,01y)\cdot 5,3-x &(1+0,01y)((1+0,01y)\cdot 5,3-x) &x\\ \hline \end{array}\)

Т.к. в итоге кредит должен быть погашен, то \((1+0,01y)((1+0,01y)\cdot 5,3-x)=x\)

Общая сумма выплат – это сумма всех платежей: \(3\cdot 0,01y\cdot 5,3+2x=8,18\)

Найдем из этого уравнения платеж \(x=\dfrac{8,18-3\cdot 0,01y\cdot 5,3}{2}\). Следовательно:

\((1+0,01y)^2\cdot 5,3-(2+0,01y)\cdot\dfrac{8,18-3\cdot 0,01y\cdot 5,3}{2}=0\)

Обозначим за \(t=0,01y\), тогда уравнение сведется к \(1325t^2+2241t-288=0 \Rightarrow t=0,12 \Rightarrow y=12 \%\)

Ответ:

\(12 \%\).

Пусть \(A\) млн рублей – первоначальный вклад. Составим таблицу:

\(\begin{array}{|l|c|c|} \hline \text{Год} & \text{Сумма в млн на счете до начисления } \% & \text{Сумма в млн на счете после начисления } \% \\ \hline 1 & A & 1,1A\\ \hline 2 & 1,1A & 1,1^2A\\ \hline 3 & 1,1^2A+1 & 1,1(1,1^2A+1)\\ \hline 4 & 1,1(1,1^2A+1)+1 & 1,1(1,1(1,1^2A+1)+1)\\ \hline \end{array}\)

Т.к. в конце четвертого года вклад должен быть больше \(10\) млн рублей, то имеем следующее неравенство:
\[1,1(1,1(1,1^2A+1)+1)>10 \Rightarrow 1,1^4A+1,1^2+1,1>10\]
Преобразовав данное неравенство, получим:

\(A>\dfrac{76900}{14641}\)

Выполнив деление в столбик до целой части, получим, что наименьшее целое \(A\), удовлетворяющее неравенству, \(A=6\).

Ответ:

\(6\) млн.

Так как строительство аквапарка должно окупиться не более, чем за \(4\) года, то прибыль за \(4\) года должна составить не менее \(40\ млн. руб.\), то есть цена \(P\) должна быть такой, чтобы существовало какое-нибудь решение неравенства

\[\begin{aligned} &4\biggl(Px - \left(\dfrac{2}{3}x^2 + 5x + 3,5\right)\biggr)\geqslant 40\qquad\Leftrightarrow\qquad Px - \left(\dfrac{2}{3}x^2 + 5x + 3,5\right)\geqslant 10\qquad\Leftrightarrow\\ \Leftrightarrow\qquad & -\dfrac{2}{3}x^2 + (P - 5)x - 3,5\geqslant 10\qquad\Leftrightarrow\qquad \dfrac{2}{3}x^2 - (P - 5)x + 13,5\leqslant 0\,. \end{aligned}\]

График левой части последнего неравенства при всяком фиксированном \(P\) представляет собой параболу с ветвями, направленными вверх. Тогда у последнего неравенства есть решение тогда и только тогда, когда вершина соответствующей параболы лежит не выше оси \(Ox\): \[y_{\text{в}} \leqslant 0\qquad\Leftrightarrow\qquad \dfrac{2}{3}\cdot\bigl(0,75(P - 5)\bigr)^2 - (P - 5)\cdot\bigl(0,75(P - 5)\bigr) + 13,5\leqslant 0\,,\] что равносильно \[\dfrac{3}{8}(P - 5)^2\geqslant 13,5\qquad\Leftrightarrow\qquad (P - 5)^2\geqslant 36\,,\] откуда с учётом условия \(P > 0\), получим: \(P\geqslant 11\).

Таким образом, минимальная цена билета, при которой аквапарк имеет шанс окупиться за 4 года (при наличии достаточного количества желающих его посетить), составляет \(P = 11\).

Ответ:

\(11\)

Фраза “долг должен быть на одну и ту же сумму меньше” означает, что кредит выплачивается дифференцированными платежами. Следовательно, т.к. кредит взят на 11 месяцев, то эта “одна и та же сумма”, на которую уменьшается долг каждый месяц, равна \(\frac1{11}\) части от суммы кредита. Обозначим сумму кредита за \(A\) и составим таблицу.
Т.к. каждый месяц долг увеличивается на \(y\%\), то в первый месяц долг увеличиться на \(0,01y\cdot A\) рублей, то есть составит \(A+0,01yA\) рублей.
После выплаты долг должен уменьшиться на \(\frac1{11}A\) рублей, то есть должен составить \(\frac{10}{11}A\) рублей. Значит, выплата в первый месяц будет равна \(A+0,01yA-\frac{10}{11}A=0,01yA+\frac1{11}A\)

\[\begin{array}{|l|c|c|c|} \hline \text{Номер месяца}&\text{Долг после начисления }\%& \text{Долг после выплаты}&\text{Выплата}\\ \hline 1& A+0,01y\cdot A& \frac{10}{11}A& 0,01y\cdot A+\frac1{11}A\\ \hline 2& \frac{10}{11}A+0,01y\cdot \frac{10}{11}A& \frac{9}{11}A& 0,01y\cdot \frac{10}{11}A+\frac1{11}A\\ \hline 3& \frac9{11}A+0,01y\cdot \frac9{11}A& \frac8{11}A& 0,01y\cdot \frac9{11}A+\frac1{11}A\\ \hline \dots&\dots&\dots&\dots\\ \hline 10& \frac2{11}A+0,01y\cdot \frac2{11}A& \frac1{11}A& 0,01y\cdot \frac2{11}A+\frac1{11}A\\ \hline 11& \frac1{11}A+0,01y\cdot \frac1{11}A& 0& 0,01y\cdot \frac1{11}A+\frac1{11}A\\ \hline \end{array}\]

Заметим, что все выплаты состоят из двух частей, причем одна часть \(\left(\frac1{11}A\right)\) фиксирована.

По условию общая сумма выплат \(R\) превысила на \(30\%\) сумму кредита \(A\). Это значит, что переплата по кредиту \(R-A\) составляет \(30\%\) от \(A\). Найдем общую сумму выплат:

\(R=\left(0,01y\cdot A+\frac1{11}A\right)+\left(0,01y\cdot \frac{10}{11}A+\frac1{11}A\right)+ \left(0,01y\cdot \frac9{11}A+\frac1{11}A\right)+\dots+\)

\(+\left(0,01y\cdot \frac2{11}A+\frac1{11}A\right)+\left(0,01y\cdot \frac1{11}A+\frac1{11}A\right)=\)

\(=0,01y\cdot A\left(1+\frac{10}{11}+\frac9{11}+\dots+\frac2{11}+\frac1{11}\right)+11\cdot \frac1{11}A=\)

В скобке — сумма 11 членов арифметической прогрессии, где \(a_1=\frac1{11}, \ a_{11}=1\). По формуле \(S_{11}=\dfrac{a_1+a_{11}}2\cdot 11\), значит

\(=0,01y\cdot A\cdot \frac12\left(\frac1{11}+1\right)\cdot 11+A=0,06yA+A\)

Тогда переплата составила \(R-A=0,06yA\). Т.к. переплата составила \(30\%\) от \(A\), то

\[\dfrac{R-A}{A}\cdot 100\%=30\% \quad \Rightarrow \quad \dfrac{0,06yA}A=0,3 \quad \Rightarrow \quad y=5\]

Ответ:

\(5\)