Компании N принадлежат две шахты в разных городах. В шахтах добываются абсолютно одинаковые минералы, но в шахте, расположенной в первом городе, используется более современное оборудование. В результате, если рабочие первой шахты трудятся суммарно \(t^2\) часов в день, то за день они добывают \(8t\) единиц минералов, а рабочие второй шахты за те же \(t^2\) часов в день добывают \(6t\) единиц минералов. За каждый час работы компания \(N\) платит каждому своему рабочему по \(100\) рублей. Компания готова выделять \(1\, 000\, 000\) рублей в день на оплату труда рабочих. Какое наибольшее количество единиц минералов можно добыть за день на этих двух шахтах?
(ЕГЭ 2015, досрочная волна)
Компания N готова оплачивать \(10000\) часов в день.
Пусть \(x^2\) часов в день суммарно трудятся рабочие первой шахты,
Пусть \(y^2\) часов в день суммарно трудятся рабочие второй шахты, тогда \[x^2 + y^2 = 10000\,.\]
Обозначим за \(S\) количество суммарно добытых за день единиц минералов, тогда \[S = 8x + 6y\]
Так как \(y = \sqrt{10000 - x^2}\), то \[S(x) = 8x + 6\sqrt{10000 - x^2}\,.\]
ОДЗ: \(x\in[-100; 100]\). Необходимо найти наибольшее значение функции \(S(x)\) при \(x\in[0; 100]\). \[S'(x) = 8 - 6\cdot\dfrac{x}{\sqrt{10000 - x^2}} = 0\]
Критические точки функции \(S(x)\) – это внутренние точки её области определения, в которых её производная равна \(0\) или не определена. \(S'(x) = 0\) при \(x = 80\).
Найдём промежутки возрастания/убывания \(S(x)\) на \([0; 100]\):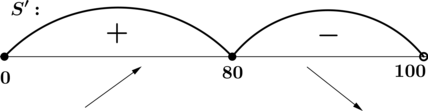
то есть \(x = 80\) точка локального максимума. Кроме того, \(S'(x)\) не определена при \(x = \pm 100\). Легко убедиться, что среди этих \(x\), попадающих на отрезок \([0; 100]\), наибольшее значение \(S(x)\) достигается при \(x = 80\). Более того, \(S(80) > S(0)\), следовательно, \(S(80)\) – наибольшее значение функции \(S(x)\) на отрезке \([0; 100]\). \[S(80) = 640 + 360 = 1000\,.\]
Ответ:
\(1000\)



