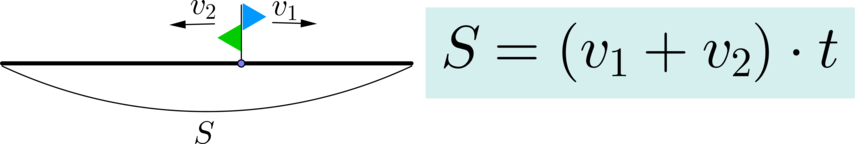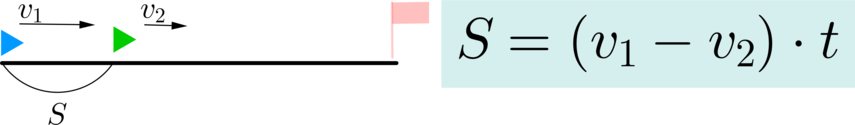Поезд длиной 1 км проходит мимо километрового столба за 1 мин, а через туннель при той же скорости – за 3 мин. Какова длина туннеля? Ответ дайте в километрах.

Из картинки видно, что “поезд проходит мимо столба” – это то же самое, что “поезд проходит расстояние, равное длине поезда”, а “поезд проходит через туннель” – это то же самое, что “поезд проходит расстояние, равное длине поезда плюс длине туннеля”.
Следовательно, так как длина поезда 1 км, а мимо столба он проходит за 1 мин, то его скорость равна 1 км/мин. Следовательно, 1 км/мин \(\cdot\) 3 мин \(=\) 3 км – длина поезда плюс длина туннеля. Следовательно, длина туннеля равна 2 км.
Ответ: 2