Из города N в город M, расстояние между которыми 36 км, выехал автомобиль со скорость 46 км/ч. Одновременно с ним из города M в том же направлении выехал другой автомобиль со скоростью 40 км/ч. Через сколько часов расстояние между автомобилями будет равно 21 км?
Если задача допускает несколько вариантов ответа, в бланк укажите их сумму.
Заметим, что так как впереди находится второй (медленный) автомобиль, то сначала автомобили будут сближаться (до того момента, как первый догонит второго), а затем будут удаляться.
Так как расстояние между ними в начале движения 36 км и \(36>21\), то первый раз расстояние в 21 км между ними будет, пока они сближаются, а второй раз – когда они будут отдаляться.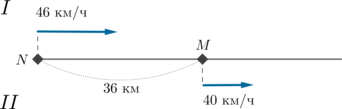
Скорость сближения автомобилей равна \(46-40=6\) км/ч. Расстояние между ними должно измениться с 36 км до 21 км, то есть на \(36-21=15\) км. Следовательно, первый раз это произойдет через \(15:6=2,5\) часа.
Теперь найдем, через сколько часов после начала движения первый догонит второго. Это значит, что расстояние между ними должно стать равным 0 км. Значит, должно измениться на 36 км. Следовательно, время встречи равно \(36:6=6\) часов.
Значит, спустя 6 часов движения картинка выглядит так:
Скорость отдаления также равна 6 км/ч. Расстояние между ними должно измениться с 0 км до 21 км, следовательно, на 21 км, следовательно, это произойдет через \(21:6=3,5\) часа после встречи. Значит, второй раз расстояние между ними будет равно 21 км через \(6+3,5=9,5\) часов.
Так как в задаче два ответа, то в бланк мы запишем \(2,5+9,5=12\)
Ответ: 12



