На рисунке изображён график функции \(y = F(x)\) – одной из первообразных некоторой функции \(y = f(x)\), определённой на интервале \((-1,1; 8,3)\). Определите по рисунку количество решений уравнения \(f(x) = 0\) на отрезке \([-1; 6]\).
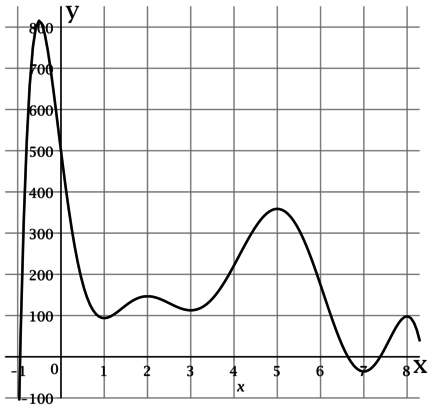
По определению первообразной \(f(x) = F'(x)\), тогда уравнение \(f(x) = 0\) равносильно \(F'(x) = 0\). Производная функции равна \(0\) в точности в тех точках, где касательная к её графику параллельна оси \(Ox\).
По рисунку видно, что на отрезке \([-1; 6]\) касательная к графику \(y = F(x)\) параллельна оси \(Ox\) в \(5\) точках (в точках с абсциссами \(x = -0,5\), \(x = 1\), \(x = 2\), \(x = 3\), \(x = 5\)).
Ответ: 5