\(\blacktriangleright\) Если производная положительна на промежутке \((a;b)\), то функция на нем строго возрастает. \(f'(x)>0 \Longrightarrow f(x) \uparrow\)

Если производная отрицательна на промежутке \((a;b)\), то функция на нем строго убывает. \(f'(x)<0 \Longrightarrow f(x) \downarrow\)

Заметим, что обратные утверждения неверны. То есть если функция строго возрастает на каком-то промежутке, то из этого не следует, что на всем этом промежутке ее производная будет положительной. Например:

функция \(f(x)=x^3\) на отрезке \([-1;1]\) строго возрастает, но ее производная не положительна всюду: в точке \(x=0\) ее производная \(f'(0)=0\) (т.к. \(f'(x)=3x^2\)).

\(\blacktriangleright\) Если функция не убывает (возрастает и/или константа) на промежутке \((a;b)\), то на этом промежутке ее производная неотрицательна (\(\geq 0\)). Верно и обратное утверждение.

\(\blacktriangleright\) Если функция не возрастает (убывает и/или константа) на промежутке \((a;b)\), то на этом промежутке ее производная неположительна (\(\leq 0\)). Верно и обратное утверждение.

\(\blacktriangleright\) В точках излома (на рисунке это точки \(A\) и \(B\)) производной не существует.

Заметим, что на промежутке \((4;+\infty)\) производная \(f'(x)=0\), т.к. на этом промежутке функция является константой (\(f(x)=10\)).

Пример: найдите количество точек, в которых производная равна нулю, если на рисунке дан график функции:

Производная равна нулю в точках \(A,B,D\), а в точке \(C\) она не существует, т.к. это точка излома.

Ознакомиться с полной теорией

Задание 8 #729

Уровень задания: Равен ЕГЭ

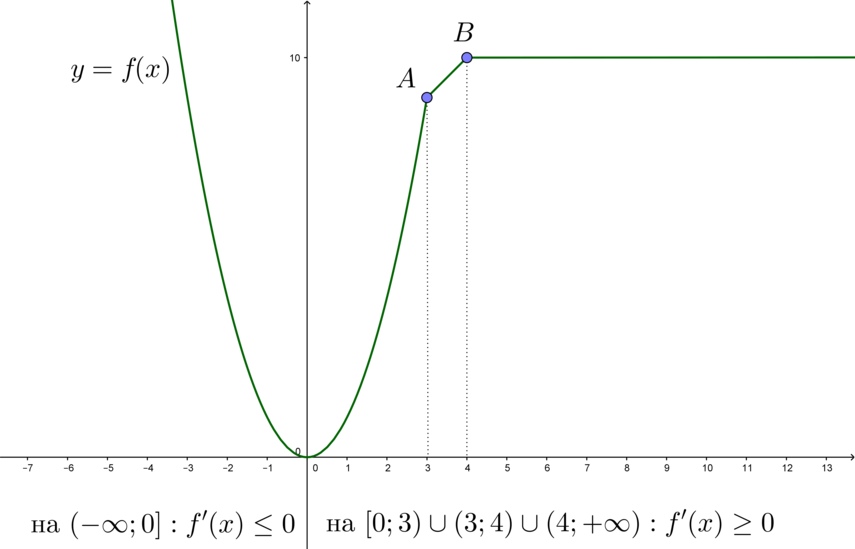
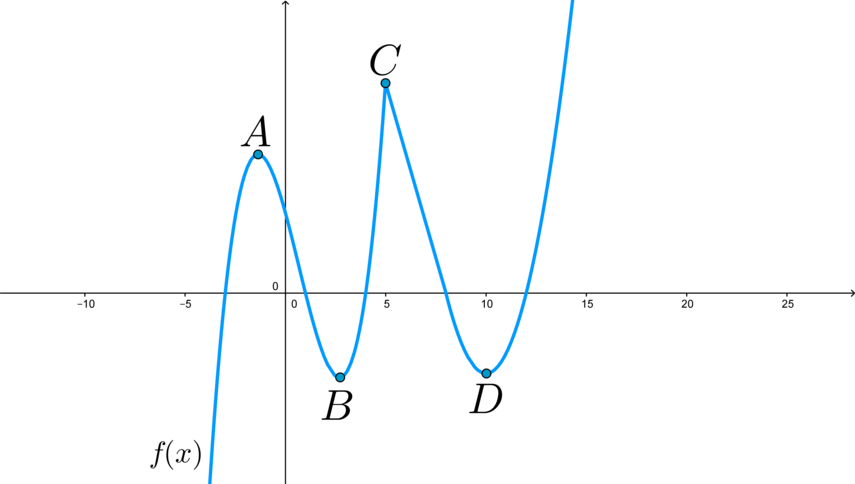
На рисунке изображен график \(y = f'(x)\) – производной функции \(y = f(x)\), определенной на интервале \((-1,5; 4,6)\). Найдите промежутки возрастания функции \(y = f(x)\). В ответе укажите длину наибольшего из них.

Показать решение

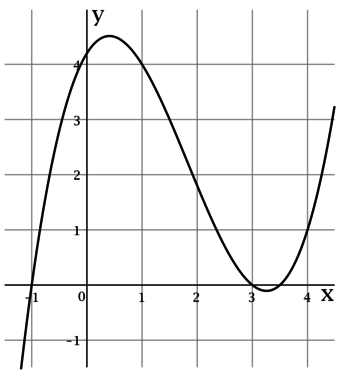
Для функции \(f(x)\), у которой производная в точке \(x_0\) имеет смысл, утверждение о том, что \(f(x)\) возрастает в \(x_0\) равносильно тому, что \(f'(x_0) > 0\).

По рисунку видно, что \(f'(x)\) положительна на промежутке \(-1 < x < 3\) и в некоторых точках промежутка \(3 < x < 4,6\), тогда \(y = f(x)\) возрастает на на промежутке \(-1 < x < 3\) и в некоторых точках промежутка \(3 < x < 4,6\), но нас интересует длина наибольшего из промежутков возрастания, а у промежутка \(-1 < x < 3\) длина больше, чем даже у промежутка \(3 < x < 4,6\), тем более она больше, чем длина части промежутка \(3 < x < 4,6\). Таким образом, длина наибольшего из промежутков возрастания равна \(4\).

Ответ: 4

1 2 cледующая
подтема