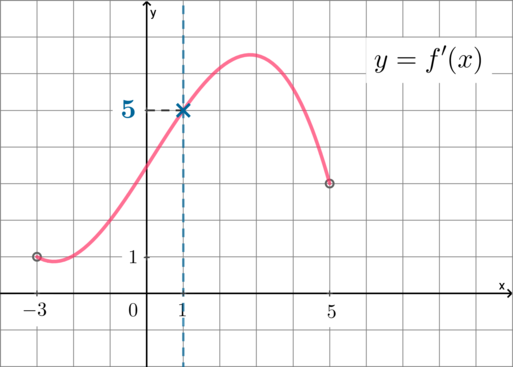
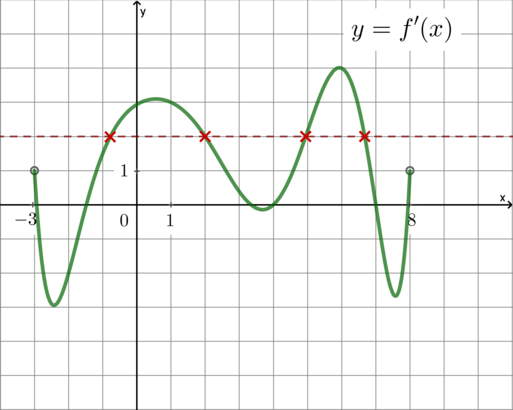
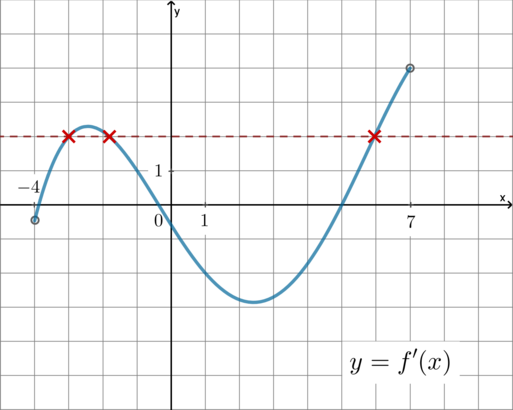
На рисунке изображен график \(y=f'(x)\) – производной функции \(f(x)\), определенной на интервале \((-3;5)\). Найдите абсциссу точки касания графика функции \(y=f(x)\) и прямой, параллельной прямой \(y=x\) или совпадающей с ней.
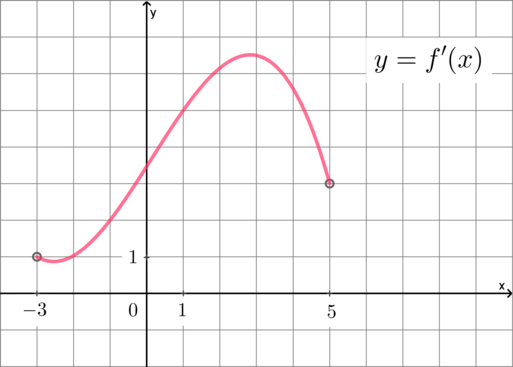
Если касательная параллельна прямой \(y=x\), то угловой коэффициент касательной равен угловому коэффициенту прямой \(y=x\), следовательно, \(k=1\). Так как \(f'(x_0)=k=1\), где \(x_0\) – точка касания, и на рисунке изображен график производной, то на графике производной нужно найти абсциссу точки, в которой \(f'(x_0)=1\), то есть ордината равна \(1\). Следовательно, это \(x_0=-2\) (заметим, что в точке \(x=-3\) производная не определена, так как в условии задачи сказано, что она определена на интервале \((-3;5)\):
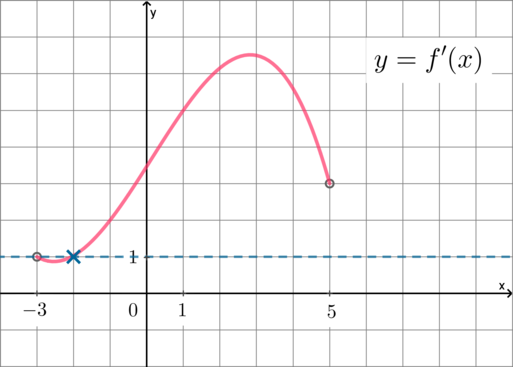
Ответ: -2