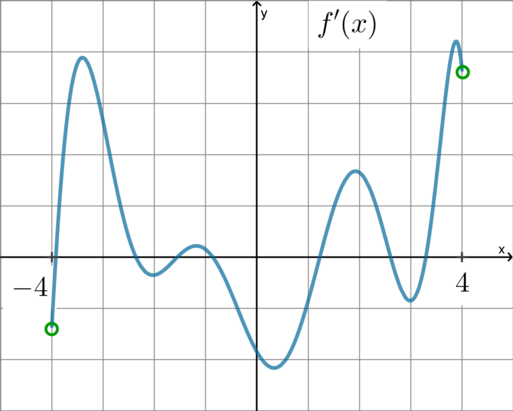
На рисунке изображен график функции \(y=f(x)\), определенной на интервале \((-5;4)\). Найдите количество точек, в которых касательная к графику функции параллельна прямой \(y=3\) или совпадает с ней.
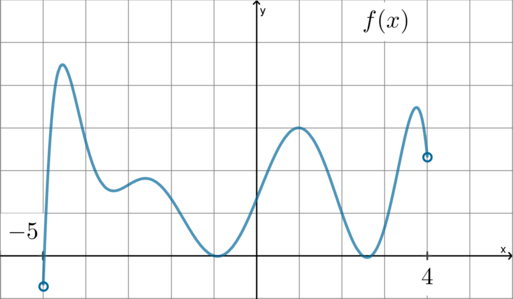
Так как на рисунке изображен график самой функции, то условие задачи нужно свести к функции.
Если касательная параллельна прямой \(y=3\), то угловой коэффициент касательной равен угловому коэффициенту прямой \(y=3\), то есть \(0\). Следовательно, \(y_k=a\), где \(a\) – некоторое число.
Если \(y_k\) – касательная к графику \(f(x)\), то ее угловой коэффициент равен \(f'(x_0)\), где \(x_0\) – абсцисса точки касания (количество таких точек нам и нужно найти).
Следовательно, \(f'(x_0)=0\).
Но производная функции равна 0 в точках экстремума, следовательно, раз у нас нарисован график самой функции, то нам нужно найти количество точек экстремума (максимума и минимума).
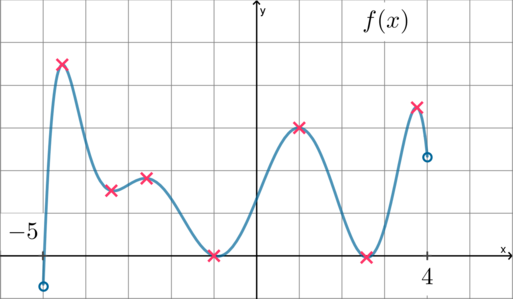
Таких точек у нас 7.
Ответ: 7