Задачи по планиметрии формата ЕГЭ (страница 3)

а) Пусть \(O\) – центр окружности, \(Q\) – точка пересечения хорд \(AC\) и \(BD\). Пусть также \(M\) и \(N\) – середины этих хорд. Тогда \(OM\) и \(ON\) – перпендикуляры к этим хордам.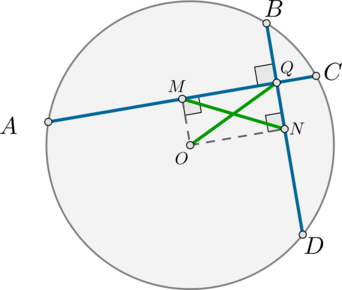

Действительно, \(\triangle AOC\) – равнобедренный (\(OA=OC\) – радиусы), поэтому медиана \(OM\) в нем является и высотой. Аналогично доказывается, что \(ON\perp BD\).

Таким образом, в четырехугольнике \(OMQN\) три угла – прямые (\(\angle M=\angle Q=\angle N=90^\circ\)), следовательно, этот четырехугольник по признаку является прямоугольником. Т.к. в прямоугольнике диагонали равны, то \(MN=OQ=3\).

б) Докажем, что \(ABCD\) – равнобедренная трапеция.
Т.к. \(AC=BD\), то \(\angle ADC=\angle BAD=\alpha\) как вписанные углы, опирающиеся на равные хорды. \(\angle BAC=\angle BDC=\beta\) как вписанные углы, опирающиеся на одну и ту же хорду \(BC\). Таким образом, \(\angle CAD=\angle BDA=\alpha-\beta\). Следовательно, равны и хорды \(AB\) и \(CD\).
Также можно сказать, что \(\angle CAD=\angle BCA\) как вписанные углы, опирающиеся на равные хорды. Следовательно, это накрест лежащие углы при \(AD\) и \(BC\) и \(AC\) – секущей. Значит, по признаку прямые \(AD\parallel BC\). Таким образом, \(ABCD\) – трапеция. А т.к. \(AB=CD\), то она равнобедренная.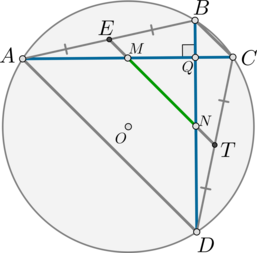

Пусть \(E\) и \(T\) – середины хорд \(AB\) и \(CD\) соответственно, то есть \(ET=5\). Тогда \(ET\) – средняя линия трапеции, следовательно, \(ET\parallel AD\parallel BC\). Тогда по теореме Фалеса прямая \(ET\) пересечет отрезки \(AC\) и \(BD\) также в серединах, следовательно, \(MN\subset ET\).

Обозначим \(AD=x, BC=y\). Тогда \(ET=\frac12\left(x+y\right)\). \(EM\) – средняя линия в \(\triangle BAC\), следовательно, \(EM=\frac12y\). Аналогично \(NT=\frac12y\) как средняя линия в \(\triangle BDC\). Тогда \(MN=ET-EM-NT=\frac12\left(x-y\right)\). Таким образом, имеем систему из двух уравнений:

\[\begin{cases} \frac12\left(x+y\right)=5\\ \frac12\left(x-y\right)=3 \end{cases}\]

Откуда находим, что \(x=AD=8\).

Ответ:

а) 3

б) 8

а) Обозначим половину угла \(DAE\) за \(\alpha\), а половину угла \(EBC\) за \(\beta\). Тогда, т.к. \(ECFD\) – параллелограмм, то \(CF\parallel ED\) и \(EC\parallel DF\).
Значит, \(\angle EBF\) и \(\angle CFB\) – накрест лежащие углы при параллельных прямых \(CF\) и \(BD\) и секущей \(BF\). Следовательно, \(\angle CFB=\beta\).

Аналогично доказывается, что \(\angle DFA=\alpha\).

Следовательно, \(\triangle BCF\) и \(\triangle ADF\) – равнобедренные, то есть \(BC=CF\) и \(AD=DF\). Но т.к. \(ABCD\) – параллелограмм, то \(BC=AD\), следовательно, \(BC=CF=AD=DF=x\).

Т.к. \(ECFD\) – параллелограмм, то \(EC=DF=x\), \(ED=CF=x\). Следовательно, \(EC=CF=FD=ED=x\). То есть \(ECFD\) – ромб.

Значит, из того, что \(BC=EC\) следует, что \(\triangle BCE\) – равнобедренный, то есть \(\angle BEC=2\beta\). Аналогично \(\triangle AED\) – равнобедренный и \(\angle AED=2\alpha\). Но \(\angle BEC\) и \(\angle AED\) – вертикальные, следовательно, \(2\beta=2\alpha\), откуда \(\alpha=\beta\).

б) Заметим также, что \(\angle ADE=\angle EBC\) как накрест лежащие при параллельных прямых \(AD\) и \(BC\) и секущей \(BD\). Следовательно, в \(\triangle AED\) все углы равны по \(2\alpha\). Значит, он равносторонний и \(2\alpha=60^\circ\).

Тогда \(\angle CED=180^\circ-2\alpha=\angle CFD\) (как противоположные углы параллелограмма), следовательно

\[\angle AFB=\angle CFD-\alpha-\alpha=180^\circ-2\alpha-2\alpha=180^\circ-4\alpha=60^\circ\]

Замечание

Заметим, что вообще говоря \(ABCD\) – прямоугольник, потому что из \(AE=ED\) следует, что и \(AC=BD\) – а равенство диагоналей параллелограмма и есть признак того, что это прямоугольник.

Ответ:

б) \(60^\circ\)

а) Пусть \(M\) и \(N\) – середины \(AB\) и \(CD\) соответственно, \(K\) – точка пересечения серединных перпендикуляров к сторонам \(AB\) и \(CD\).

Из точки \(A\) на прямую, содержащую \(CD\), опустим перпендикуляр \(AC'\). Из точки \(D\) на прямую, содержащую \(AB\), опустим перпендикуляр \(DB'\).

Так как \(\angle A = \angle D\), то треугольники \(AB'D\) и \(AC'D\) равны по гипотенузе и острому углу, откуда \(C'D = AB'\). Обозначим \(C'D = h\). Возможны 2 случая:

1) отрезок \(BC\) пересекает \(B'C'\),

2) отрезок \(BC\) не пересекает \(B'C'\).

1) Пусть \(BB' = a\), \(CC' = b\) и \(AB' > AB\), тогда \(C'D < CD\).
\(AB = h - a\), \(CD = h + b\), откуда \[AM = \dfrac{h - a}{2},\qquad DN = \dfrac{h + b}{2}.\]

Треугольники \(AMK\) и \(AB'D\) подобны по двум углам, откуда \[\dfrac{h - a}{2h} = \dfrac{AK}{AD}\qquad\Rightarrow\qquad AK = \dfrac{h - a}{2h}AD.\]

Аналогично из подобия треугольников \(KND\) и \(AC'D\) получаем \(DK = \dfrac{h + b}{2h}AD\).

Так как \(AK + KD = AD\), то \[AD = \dfrac{h - a}{2h}AD + \dfrac{h + b}{2h}AD,\] откуда \[-a + b = 0\qquad\Rightarrow\qquad a = b.\]

Так как треугольники \(AB'D\) и \(AC'D\) равны (по гипотенузе и острому углу), то \(B'D = A'C\). Так как \(BB' = CC'\), то прямоугольные треугольники \(BB'D\) и \(ACC'\) равны (по двум катетам), следовательно, \(AC = BD\).

2) Аналогично первому случаю, только в итоге получим \[AD = \dfrac{h - a}{2h}AD + \dfrac{h - b}{2h}AD\] или \[AD = \dfrac{h + a}{2h}AD + \dfrac{h + b}{2h}AD.\] В обоих этих случаях будет \(a + b = 0\), откуда в силу \(a\geq 0\), \(b\geq 0\) получим, что \(a = b = 0\), но \(BD' = AC'\) (так как треугольники \(AB'D\) и \(AC'D\) равны).

В итоге \(AC = BD\), тогда из теоремы о биссектрисе (биссектриса треугольника делит его сторону на отрезки, пропорциональные прилежащим сторонам) получаем нужное равенство.

б) Так как у треугольников \(BDA\) и \(CDA\) основание \(AD\) – общее, то \[\dfrac{\rho(B; AD)}{\rho(C; AD)} = \dfrac{S_{\triangle BDA}}{S_{\triangle CDA}}.\]

Так как \(AC = BD\), а \(AD\) общая для треугольников \(BDA\) и \(CDA\), то \[\dfrac{S_{\triangle BDA}}{S_{\triangle CDA}} = \dfrac{\sin\alpha}{\sin\beta}.\] В итоге \[\dfrac{\rho(B; AD)}{\rho(C; AD)} = \dfrac{\sin\alpha}{\sin\beta}.\]

Ответ:

б) \(\dfrac{\sin\alpha}{\sin\beta}\).

а) Пусть \(M\) и \(N\) – середины \(AB\) и \(CD\) соответственно, \(K\) – точка пересечения серединных перпендикуляров к сторонам \(AB\) и \(CD\).

Из точки \(A\) на прямую, содержащую \(CD\), опустим перпендикуляр \(AC'\). Из точки \(D\) на прямую, содержащую \(AB\), опустим перпендикуляр \(DB'\).

Так как \(\angle A = \angle D\), то треугольники \(AB'D\) и \(AC'D\) равны по гипотенузе и острому углу, откуда \(C'D = AB'\). Обозначим \(C'D = h\). Возможны 2 случая:

1) отрезок \(BC\) пересекает \(B'C'\),

2) отрезок \(BC\) не пересекает \(B'C'\).

1) Пусть \(BB' = a\), \(CC' = b\) и \(AB' > AB\), тогда \(C'D < CD\).
\(AB = h - a\), \(CD = h + b\), откуда \[AM = \dfrac{h - a}{2},\qquad DN = \dfrac{h + b}{2}.\]

Треугольники \(AMK\) и \(AB'D\) подобны по двум углам, откуда \[\dfrac{h - a}{2h} = \dfrac{AK}{AD}\qquad\Rightarrow\qquad AK = \dfrac{h - a}{2h}AD.\]

Аналогично из подобия треугольников \(KND\) и \(AC'D\) получаем \(DK = \dfrac{h + b}{2h}AD\).

Так как \(AK + KD = AD\), то \[AD = \dfrac{h - a}{2h}AD + \dfrac{h + b}{2h}AD,\] откуда \[-a + b = 0\qquad\Rightarrow\qquad a = b.\]

Так как треугольники \(AB'D\) и \(AC'D\) равны (по гипотенузе и острому углу), то \(B'D = A'C\). Так как \(BB' = CC'\), то прямоугольные треугольники \(BB'D\) и \(ACC'\) равны (по двум катетам), следовательно, \(AC = BD\).

2) Аналогично первому случаю, только в итоге получим \[AD = \dfrac{h - a}{2h}AD + \dfrac{h - b}{2h}AD\] или \[AD = \dfrac{h + a}{2h}AD + \dfrac{h + b}{2h}AD.\] В обоих этих случаях будет \(a + b = 0\), откуда в силу \(a\geq 0\), \(b\geq 0\) получим, что \(a = b = 0\), но \(BD' = AC'\) (так как треугольники \(AB'D\) и \(AC'D\) равны).

В итоге \(AC = BD\), тогда из теоремы о биссектрисе (биссектриса треугольника делит его сторону на отрезки, пропорциональные прилежащим сторонам) получаем нужное равенство.

б) Так как у треугольников \(BDA\) и \(CDA\) основание \(AD\) – общее, то \[\dfrac{\rho(B; <AD>)}{\rho(C; <AD>)} = \dfrac{S_{\triangle BDA}}{S_{\triangle CDA}}.\]

Так как \(AC = BD\), а \(AD\) общая для треугольников \(BDA\) и \(CDA\), то \[\dfrac{S_{\triangle BDA}}{S_{\triangle CDA}} = \dfrac{\sin\alpha}{\sin\beta}.\] В итоге \[\dfrac{\rho(B; <AD>)}{\rho(C; <AD>)} = \dfrac{\sin\alpha}{\sin\beta}.\]

Ответ:

б) \(\dfrac{\sin\alpha}{\sin\beta}\).

а) Проведем радиусы \(OR\), \(OT\) и радиус \(OE\) в точку \(E\) касания окружности со стороной \(BC\), а также соединим \(A\) и \(O\).

Тогда \(OE\) перпендикулярно \(BC\) и значит точки \(B\), \(O\) и \(T\) лежат на одной прямой, откуда \(\angle BOE = \angle TOS\) как вертикальные, следовательно треугольники \(BOE\) и \(TOS\) равны по катету и острому углу (\(TO = OE\) как радиусы).

Тогда \(BO = OS\). \(AO\) – биссектриса в треугольнике \(ABS\) (она проходит через точку, равноудаленную от сторон угла \(\angle BAS\)), но из равенства \(BO = OS\) следует, что \(AO\) – медиана.

Треугольник, в котором биссектриса является медианой – равнобедренный и \(AO\) перпендикулярна \(BS\).

\(AR = AT\) как отрезки касательной, проведенной из одной точки, тогда треугольники \(ARO\) и \(AOT\) – равны (по трем сторонам), тогда \(\angle AOR = \angle AOT\) и \(AO\) – биссектриса угла \(\angle ROT\).

Треугольник \(ROT\) равнобедренный, тогда \(AO\) перпендикулярна \(RT\). В итоге, \(AO\) перпендикулярна \(RT\) и \(BS\), тогда \(RT \parallel BS\).

б) Пусть \(OK\) – перпендикуляр из точки \(O\) на \(CD\). Средняя линия трапеции \(BCDS\) является средней линией трапеции \(ECTD\).

Так как средняя линия трапеции равна полусумме оснований, то \[EC + TD = 2\cdot 4 = 8.\] \(CD = EC + TD = 8\) (так как отрезки касательных, проведенных из одной точки равны, то \(EC = CK\), а \(TD = DK\)). \[S_{COD} = \dfrac{1}{2}CD\cdot OK = 16,\] откуда \(OK = 4\), следовательно \(OK\) и есть средняя линия трапеции \(BCDS\) (перпендикуляр из точки на прямую имеет наименьшую длину, другой отрезок, соединяющий \(O\) и точку на \(CD\) был бы длиннее).

\(OK\) перпендикулярен \(CD\), но \(OK \parallel AD\), тогда \(ABCD\) – прямоугольная трапеция, \(\angle ADC = 90^{\circ}\). В итоге \(OECK\) – прямоугольник, у которого \(OE = OK = 4\), тогда он квадрат и \(OK = CK = 4\).

Треугольник \(COK\) – прямоугольный, тогда \(CO = 4\sqrt{2}\).

Ответ:

б) \(4\sqrt{2}\).

а) Так как стороны треугольника \(ABC\) образуют арифметическую прогрессию, то их длины можно представить в виде \(a\), \(a + d\), \(a + 2d\), где \(d > 0\) – натуральное.

Используя формулу Герона, можно получить равенство \[p\cdot r = S_{\triangle ABC} = \sqrt{p(p - a)(p - (a + d))(p - (a + 2d))},\] где \(p = \dfrac{3a + 3d}{2}\) – полупериметр, откуда \[12(a + d)\cdot r^2 = (a + 3d)(a + d)(a - d)\qquad\Rightarrow\qquad 12\cdot r^2 = (a + 3d)(a - d) = a^2 + 2ad - 3d^2,\] то есть \(a^2 + 2ad - 3(d^2 + 4r^2) = 0\), откуда \[a = -d\pm \sqrt{4d^2 + 12r^2},\] но при учёте \(a > 0\), получим \(a = \sqrt{4d^2 + 12r^2} - d\).

Пусть \(r = \dfrac{1}{2}\), тогда \(a = \sqrt{4d^2 + 3} - d\), откуда \(\sqrt{4d^2 + 3}\) – целое (следовательно, натуральное, ведь \(4d^2 > 0\)) число, то есть \(\sqrt{4d^2 + 3} = k\), где \(k\) – натуральное.

\(4d^2 + 3 = k^2\), откуда \[3 = (k - 2d)(k + 2d),\] то есть \(k + 2d\) – натуральный делитель числа \(3\) при том, что \(k\) и \(d\) натуральные, откуда \(k = d = 1\), но тогда \[(k - 2d)(k + 2d) = -3\neq 3.\] Полученное противоречие завершает доказательство.

б) Так как \(r = 1\), то \(a = \sqrt{4d^2 + 12} - d\), откуда \(\sqrt{4d^2 + 12}\) – целое (следовательно, натуральное) число, то есть \(\sqrt{4d^2 + 12} = k\), где \(k\) – натуральное.

\(4d^2 + 12 = k^2\), откуда \[12 = (k - 2d)(k + 2d).\] Так как \(k\) и \(d\) натуральные, то \(k - 2d\) целое, а \(k + 2d\) – натуральное, следовательно, число \(k - 2d\) – целое положительное (иначе его произведение с \(k + 2d\) отрицательно, но \(12 > 0\)), то есть натуральное число.

\[k + 2d - (k - 2d) = 4d\] – делится на \(4\). Среди всевозможных пар натуральных чисел, в произведнии дающих \(12\), только пара \(\{6; 2\}\) подходит под последнее условие, следовательно, \(d = 1\), \(k = 4\), что подходит, тогда \(a = 3\).

При этом у треугольника с длинами сторон \(3\), \(4\) и \(5\) площадь равна \(6\), следовательно, \(r = 1\) – подходит под условие, тогда периметр \(ABC\) равен \(12\).

Ответ:

б) \(12\).