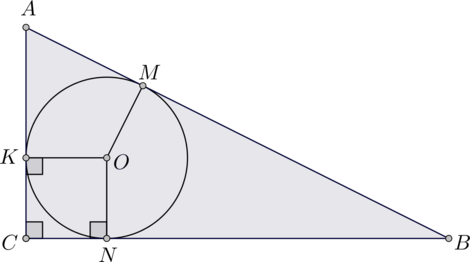
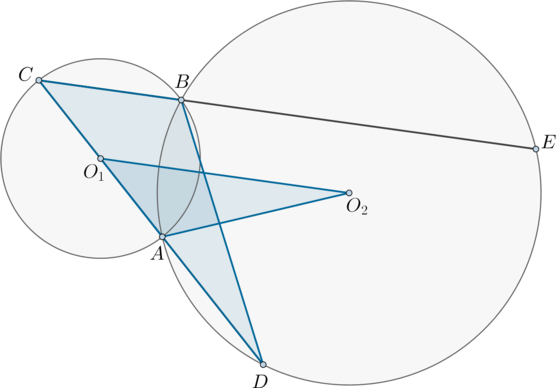
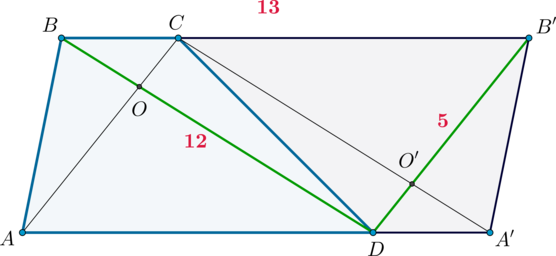
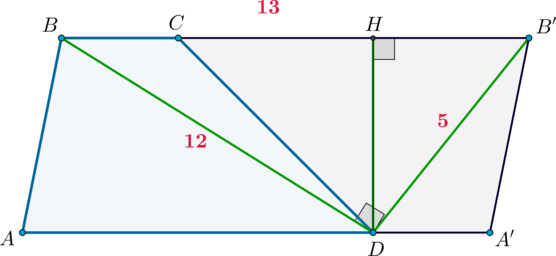
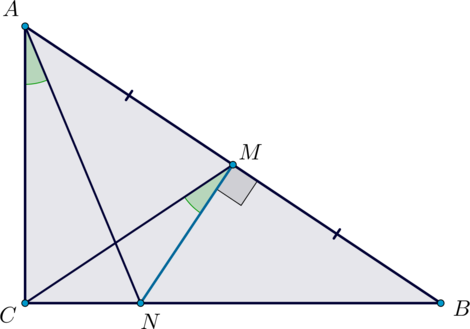
В трапецию \(ABCD\) с большим основанием \(AD\) вписана окружность, которая касается боковых сторон \(AB\) и \(CD\) в точках \(N\) и \(M\) соответственно, причем \(AN:NB=8:1\), \(DM:MC=2:1\).
а) Докажите, что \(AD=4BC\).
б) Найдите \(MN\), если известно, что радиус данной окружности равен \(\sqrt6\).
(ЕГЭ 2017, резервный день)
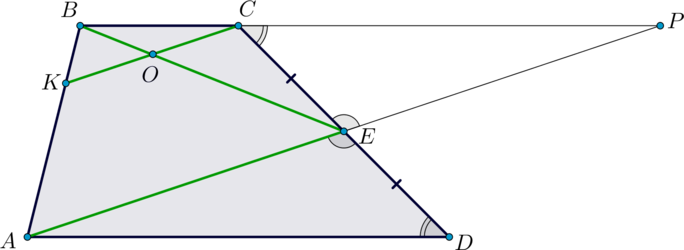
а) Продлим боковые стороны трапеции до пересечения в точке \(P\).
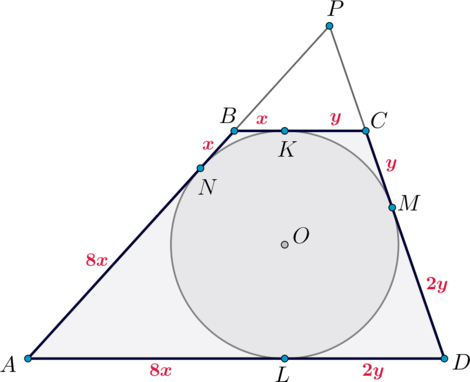
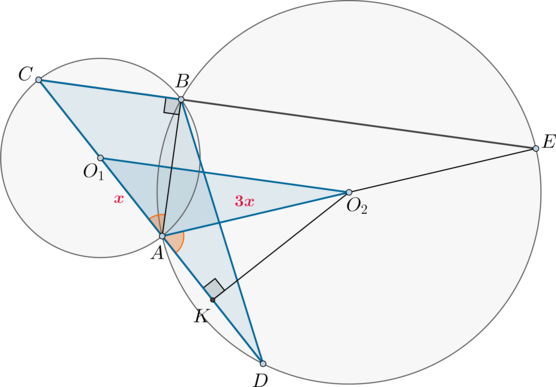
Так как \(AN:NB=8:1\), то можно принять \(AN=8x, NB=x\). Аналогично \(CM=y, MD=2y\). Так как отрезки касательных, проведенных из одной точки к окружности, равны, то \(BK=x, CK=y, AL=8x, LD=2y\), где \(K, L\) – точки касания окружности с основаниями.
Аналогично \(PN=PM\) как отрезки касательных, проведенных из одной точки к окружности.
Так как \(\triangle APD\sim \triangle BPC\) по двум углам, то \[\dfrac{PA}{PB}=\dfrac{AD}{BC}\quad\Rightarrow\quad
\dfrac{PB+AB}{PB}=\dfrac{AD}{BC}\quad\Rightarrow\quad
PB=\dfrac{AB\cdot BC}{AD-BC}=\dfrac{9x\cdot (x+y)}{8x+2y-x-y}\] По той же причине \[\dfrac{PD}{PC}=\dfrac{AD}{BC}\quad\Rightarrow\quad
\dfrac{PC+CD}{PC}=\dfrac{AD}{BC}\quad\Rightarrow\quad PC=
\dfrac{3y\cdot (x+y)}{7x+y}\] Так как \(PN=PM\), то \[x+\dfrac{9x\cdot (x+y)}{7x+y}=y+\dfrac{3y\cdot (x+y)}{7x+y}
\quad\Leftrightarrow\quad 4x^2=y^2\quad\Rightarrow\quad y=2x\] Таким образом, \(AD=12x\), \(BC=3x\), то есть \(AD=4BC\).
б) Из пункта а) следует, что \(PB=3x, PC=2x\). Обозначим \(\angle
APD=\alpha\).
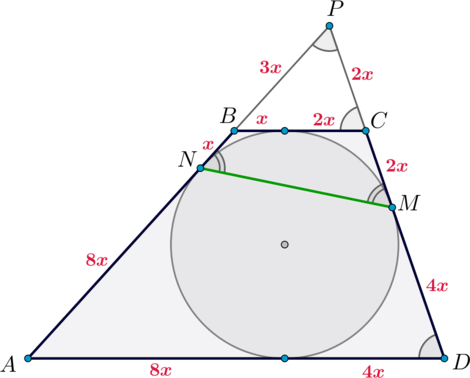
Тогда по теореме косинусов из \(\triangle NPM\): \[MN=\sqrt{(4x)^2+(4x)^2-2\cdot 4x\cdot 4x\cdot \cos\alpha}=
4x\cdot \sqrt{2-2\cos\alpha}\] Найдем \(x\) и \(\cos \alpha\). По теореме косинусов из \(\triangle APD\): \[AD^2=AP^2+DP^2-2\cdot AP\cdot DP\cdot \cos\alpha
\quad\Rightarrow\quad \cos\alpha=\dfrac{64x^2}{2\cdot 12x\cdot
8x}=\dfrac13\quad\Rightarrow\quad \sin \alpha=\dfrac{2\sqrt2}3\] По формуле \(S=p\cdot r\) для \(\triangle APD\): \[\dfrac 12\cdot AP\cdot DP\cdot \sin \alpha=\dfrac{AP+PD+AD}2\cdot
\sqrt6
\quad\Rightarrow\quad x=\dfrac{\sqrt3}2\] Таким образом, \[MN=4\]
Ответ:
б) \(4\)