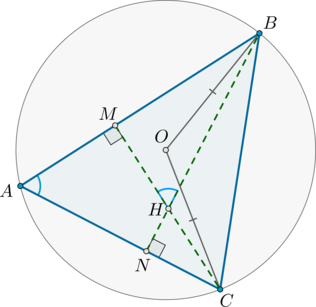
В треугольнике \(ABC\) угол \(C\) равен \(45^\circ\), угол \(A\) равен \(60^\circ\). Точки \(A_1\), \(B_1\), \(C_1\) – середины сторон \(BC\), \(AC\), \(AB\) соответственно. \(AK\) – высота.
а) Докажите, что точки \(A_1, B_1, C_1, K\) лежат на одной окружности.
б) Найдите \(A_1K\), если \(BC=2\sqrt3\).
(ЕГЭ 2017, досрочная волна)
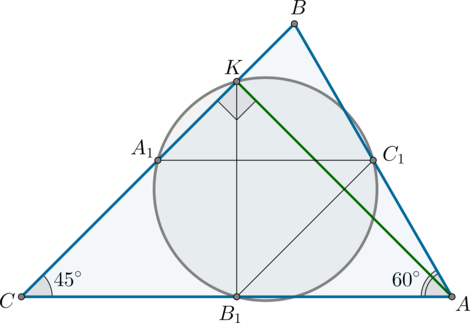
а) Проведем \(A_1C_1\), \(C_1B_1\). Так как \(A_1C_1\) – средняя линия в \(\triangle ABC\), то \(A_1C_1=\frac12CA=CB_1\). Также \(A_1C_1\parallel CB_1\). Следовательно, \(CA_1C_1B_1\) – параллелограмм. Значит, \(\angle A_1C_1B_1=\angle A_1CB_1=45^\circ\).
Заметим, что \(K\) будет лежать на отрезке \(A_1B\) по теореме о расположении медианы и высоты, опущенных из одной вершины (высота будет лежать между медианой \(AA_1\) и \(AB\), так как \(AB<AC\)).
Проведем \(KB_1\). Так как \(\triangle CKA\) прямоугольный и один из острых углов равен \(45^\circ\), то он равнобедренный, следовательно, \(KB_1\) не только медиана в нем, но и высота. Следовательно, \(\triangle CKB_1\) также прямоугольный и один из его углов равен \(45^\circ\), следовательно, и \(\angle CKB_1=45^\circ\).
Таким образом, \(\angle A_1C_1B_1=\angle A_1KB_1=45^\circ\), значит, около четырехугольника \(A_1KC_1B_1\) можно описать окружность. Это и значит, что точки \(A_1, B_1,C_1, K\) лежат на одной окружности.
б) По теореме синусов в \(\triangle ABC\): \[\dfrac{BC}{\sin\angle A}=\dfrac{AB}{\sin\angle C} \quad\Rightarrow\quad
\dfrac{2\sqrt3}{\frac{\sqrt3}2}=\dfrac{AB}{\frac{\sqrt2}2}
\quad\Rightarrow\quad AB=2\sqrt2.\] 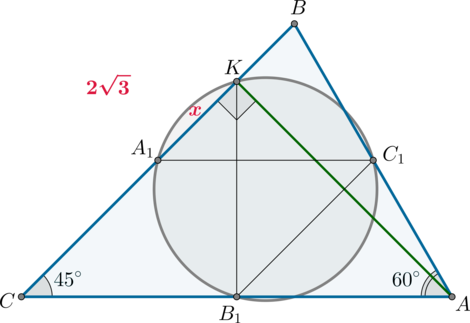
Обозначим \(A_1K=x\). Тогда \(AK=CK=\sqrt3+x\). Тогда по теореме Пифагора из \(\triangle AKB\): \[KB^2=8-(x+\sqrt3)^2\] Заметим, что \(A_1K+KB=A_1B=\sqrt3\), следовательно, \(KB=\sqrt3-x\), следовательно, получаем уравнение: \[8-(x+\sqrt3)^2=(\sqrt3-x)^2 \quad\Rightarrow\quad x=1.\]
Ответ:
б) 1