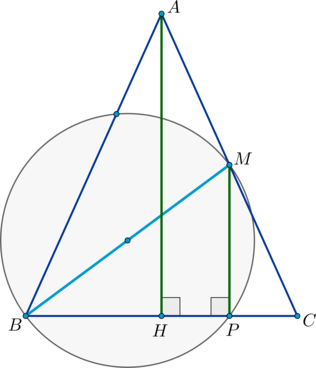
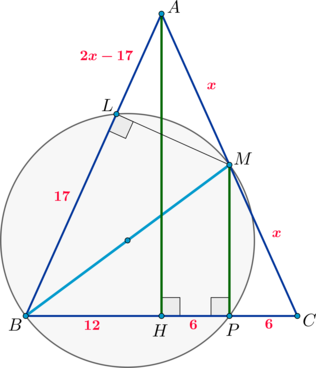
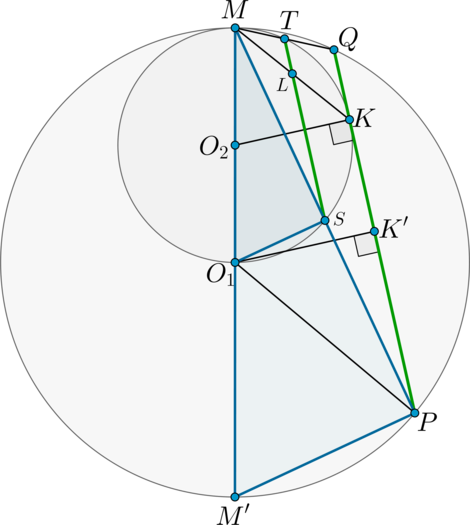
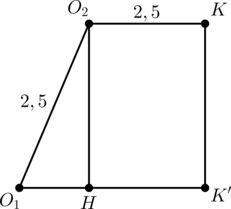
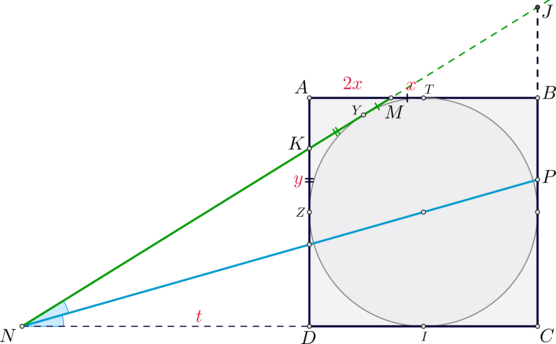
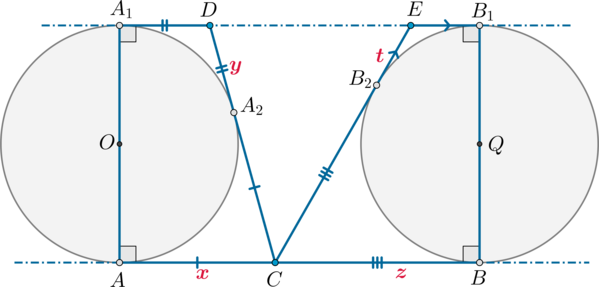
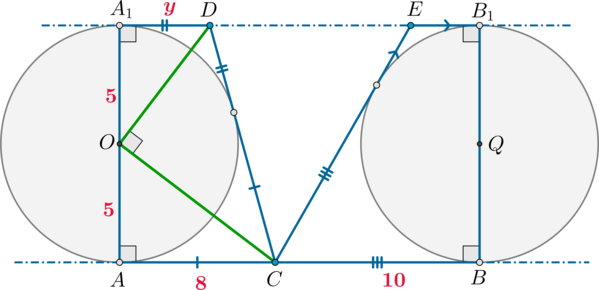
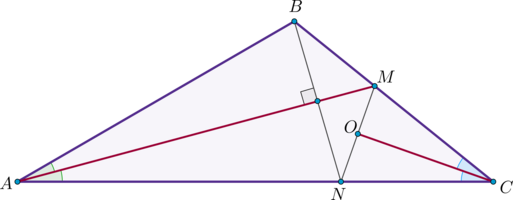
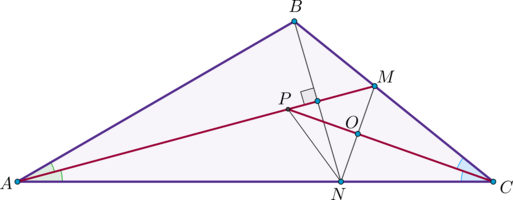
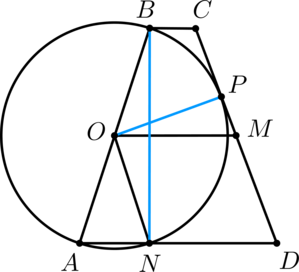Точка \(P\) лежит на стороне \(AB\) выпуклого четырёхугольника \(ABCD\), причём \(A\) и \(B\) – вершины равнобедренных треугольников с основаниями \(PD\) и \(PC\) соответственно. При этом \(PD\perp PC\).
а) Докажите, что биссектрисы углов \(DAP\) и \(PBC\) пересекаются на стороне \(CD\).
б) Пусть \(Q\) – точка пересечения этих биссектрис. Найдите площадь четырёхугольника, стороны которого лежат на прямых \(AQ\), \(PD\), \(PC\), \(QB\), если известно, что \(AP : AB = 2 : 9\) и \(S_{ABCD} = 1\).
(ЕГЭ 2015, резервный день)
а) Пусть \(Q\) – точка пересечения биссектрисы угла \(DAP\) со стороной \(CD\). Пусть \(S\) – точка пересечения \(AQ\) и \(PD\). Так как \(DA = AP\), то \(AQ\) содержит медиану и высоту в треугольнике \(DAP\), откуда следует, что \(AQ\perp DP\) и \(S\) – середина \(DP\).
Таким образом, \(QS\) – медиана и высота в треугольнике \(QPD\), следовательно, треугольник \(QPD\) равнобедренный и \(PQ = QD\).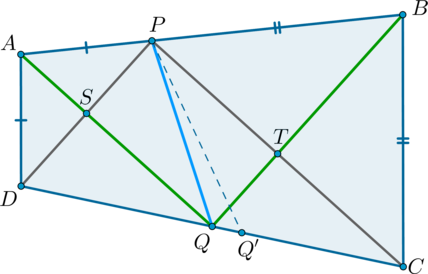
Треугольник \(DPC\) – прямоугольный. Предположим, что некоторая точка \(Q'\neq Q\) – середина \(CD\), тогда \(PQ' = DQ'\) (\(PQ'\) – медиана, проведённая к гипотенузе), следовательно, \(\angle PDQ = \angle DPQ'\), но \(\angle PDQ = \angle DPQ\), следовательно, точки \(P\), \(Q\) и \(Q'\) лежат на одной прямой, то есть \(Q'\) лежит на \(PQ\), а также \(Q'\) лежит на \(CD\). Но две не совпадающие прямые могут иметь не более одной общей точки, следовательно, наше предположение неверно и \(Q\) – середина \(CD\).
Тогда \(PQ = QC\), следовательно, \(\triangle PQB = \triangle CQB\) (по трём сторонам), откуда получаем, что \(QB\) – биссектриса угла \(PBC\), то есть \(Q\) – точка пересечения биссектрис углов \(DAP\) и \(PBC\). Так как двух точек пересечения у несовпадающих прямых быть не может, то биссектрисы углов \(DAP\) и \(PBC\) пересекаются на стороне \(CD\) (в точке \(Q\)).
б) В четырёхугольнике \(PSQT\): \(\angle SPT = 90^\circ = \angle PSQ = \angle PTQ\), следовательно, \(\angle SQT = 360^\circ - 270^\circ = 90^\circ\) и \(PSQT\) – прямоугольник.
Рассмотрим прямоугольные треугольники \(ASP\) и \(AQB\): \(\angle BAQ\) – общий, следовательно, треугольники \(ASP\) и \(AQB\) подобны по острому углу, следовательно, \[\dfrac{PS}{BQ} = \dfrac{AP}{AB} = \dfrac{2}{9}\,,\] но \(PS = QT\), тогда \[\dfrac{QT}{BQ} = \dfrac{2}{9}\qquad\Rightarrow\qquad BT = \dfrac{7}{2}\cdot QT\,.\]
Аналогично треугольники \(BPT\) и \(BAQ\) подобны, откуда \[\dfrac{AQ}{PT} = \dfrac{AB}{PB} = \dfrac{9}{7}\,,\] но \(PT = QS\), тогда \[\dfrac{AQ}{QS} = \dfrac{9}{7}\qquad\Rightarrow\qquad AS = \dfrac{2}{7}\cdot QS\,.\]
\[\begin{aligned} &S_{ABCD} = S_{DAP} + S_{DPC} + S_{PBC} = AS\cdot PS + 2PS\cdot PT + PT\cdot BT =\\ = \,&\dfrac{2}{7}\cdot QS\cdot PS + 2PS\cdot PT + PT\cdot \dfrac{7}{2}\cdot QT = \dfrac{81}{14}\cdot S_{PSQT}\,, \end{aligned}\]
следовательно, \[1 = \dfrac{81}{14}\cdot S_{PSQT}\qquad\Rightarrow\qquad S_{PSQT} = \dfrac{14}{81}\,.\]
Ответ:
б) \(\dfrac{14}{81}\)