Задачи по планиметрии прошлых лет (страница 6)

а) Пусть \(O\) – центр окружности, описанной около \(\triangle KLN\). Так как \(LM\) – касательная к окружности, проходящей через точку \(L\), то \(LM\perp OL\), следовательно, \(OL\perp KN\). Опустим из точки \(O\) на \(KN\) перпендикуляр \(OP\).

Так как центр описанной около треугольника окружности – это точка пересечения его серединных перпендикуляров, то \(P\) – середина \(KN\).

Точки \(P\), \(O\) и \(L\) лежат на одной прямой: в самом деле, \(LO\perp KN\perp OP\), тогда прямые, содержащие \(LO\) и \(OP\) либо параллельны, либо совпадают, но они проходят через общую точку \(O\).

Таким образом, \(L\) лежит на серединном перпендикуляре к \(KN\), следовательно, \(L\) равноудалена от концов отрезка \(KN\) и треугольник \(KLN\) – равнобедренный (\(KL = LN\)). Кроме того, \(\angle KLO = \angle OLN\).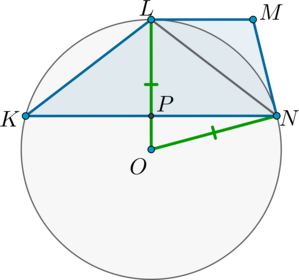

Аналогично, \(ON\perp MN\). Так как сумма углов четырёхугольника равна \(360^\circ\), то \(\angle LON + \angle LMN = 180^\circ\), причём \[\angle LON = 180^\circ - \angle OLN - \angle ONL = 180^\circ - 2\angle OLN = 180^\circ - \angle KLN,\] откуда следует, что \(\angle LMN = \angle KLN\).

Кроме того, \(\angle LNK = \angle NLM\) как внутренние накрест лежащие при параллельных прямых \(KN\), \(LM\) и секущей \(LN\). В итоге, два угла треугольника \(LMN\) соответственно равны двум углам треугольника \(KLN\), следовательно, они подобны.

Замечание. Формально в рамках пункта а) треугольник \(KLN\) может быть и остроугольным, а на рисунке он тупоугольный, однако, все рассуждения, приведённые выше, будут справедливы и для случая остроугольного треугольника \(KLN\).

б) \(\angle KLN = \angle LMN = 120^\circ\), тогда \(\angle LKN = \angle LNK = 30^\circ\). \[LP = KP\cdot \mathrm{tg}\ \! 30^\circ = 3\cdot\dfrac{1}{\sqrt{3}} = \sqrt{3}.\] В итоге \[S_{\triangle KLN} = \dfrac{1}{2}\cdot KN\cdot LP = 3\cdot \sqrt{3} = 3\sqrt{3}.\]

Ответ:

б) \(3\sqrt{3}\)

а) Так как \(ABCD\) – квадрат, то \(BC = AD\), следовательно, достаточно доказать, что \(CK\cdot CE = BC^2\), что (в силу \(BC > 0\)) равносильно \(\dfrac{CK}{BC}=\dfrac{BC}{CE}\).

Таким образом, достаточно доказать подобие треугольников \(BCE\) и \(BCK\), а также равенства \[\angle CBD = \angle BEC,\qquad \angle BKC = \angle CBE.\]

В треугольниках \(BCE\) и \(BCK\) \(\angle BCE\) – общий. Покажем, что \(\angle BEC = \angle CBD\):
так как равные хорды стягивают равные дуги, то \(\smile BC = \smile CD\), тогда углы \(\angle BEC\) и \(\angle CBD\) равны как вписанные углы, опирающиеся на равные дуги.

Таким образом, треугольники \(BCE\) и \(BCK\) подобны. Остаётся убедиться в том, что \(\angle BKC = \angle CBE\), что верно, так как сумма углов треугольника равна \(180^\circ\), следовательно, \[\angle BKC = 180^\circ - \angle BCE - \angle CDB = 180^\circ - \angle BCE - \angle BEC = \angle CBE.\]

б) \(\angle BCE = 90^\circ - \angle ECD = 15^\circ\),
\(\angle BEC = \angle CBD = 45^\circ\) (так как диагональ квадрата \(BD\) – биссектриса угла \(\angle ABC\)),
\(\angle CBE = \angle BKC = 180^\circ - \angle BCE - \angle CDB = 120^\circ\),
\(\angle BKE = 180^\circ - \angle BKC = 60^\circ\),
\(\angle EBK = \angle CBE - \angle CBD = 75^\circ\).

Из теоремы синусов для треугольника \(BCE\) следует, что \[\dfrac{CE}{\sin 120^\circ} = \dfrac{BE}{\sin 15^\circ}\qquad\Rightarrow\qquad BE = \sin 15^\circ\cdot\dfrac{CE}{\sin 120^\circ}.\]

Из теоремы синусов для треугольника \(BEK\) следует, что \[\dfrac{EK}{\sin 75^\circ} = \dfrac{BE}{\sin 60^\circ}\qquad\Rightarrow\qquad EK = \sin 75^\circ\cdot\dfrac{BE}{\sin 60^\circ} = \sin 75^\circ\cdot\dfrac{\sin 15^\circ\cdot\dfrac{CE}{\sin 120^\circ}}{\sin 60^\circ},\] откуда \[\dfrac{CE}{EK} = \dfrac{\sin 120^\circ\cdot\sin 60^\circ}{\sin 75^\circ\cdot\sin 15^\circ}.\] Так как \(\sin\alpha\cdot\sin\beta = 0,5\cdot\bigl(\cos(\alpha - \beta) - \cos(\alpha + \beta)\bigr)\), то \[\dfrac{CE}{EK} = \dfrac{0,5\cdot(0,5 + 1)}{0,5\cdot 0,5} = 3\quad \Rightarrow\quad CK:KE=2:1\]

Ответ:

б) \(2:1\)

а) Покажем, что точка \(M\) – основание высоты, построенной из точки \(C\) на \(AB\). Опустим из точки \(C\) на \(AB\) высоту \(CM'\).

Пусть \(O_1\) и \(O_2\) – центры окружностей с диаметрами \(AC\) и \(BC\) соответственно. Так как \(\triangle ACM'\) – прямоугольный, то \(O_1M' = AO_1\).

Аналогично \(O_2M' = CO_2\). Таким образом, точка \(M'\) лежит на окружности с диаметром \(AC\) и лежит на окружности с диаметром \(BC\), следовательно, она есть точка пересечения этих окружностей.

Так как две не совпадающие окружности имеют не более двух общих точек, то \(M' = M\).

\(\angle CMP\) дополняет \(\angle PMB\) до прямого, тогда достаточно показать, что \[\angle CMP = \angle QMB.\] Углы \(QMB\) и \(QCB\) – вписанные, опирающиеся на одну дугу, тогда \(\angle QCB = \angle QMP\).

Аналогично \(\angle CAP = \angle CMP\). Таким образом, достаточно показать, что \[\angle QCB = \angle CAP.\]

Так как \(P\) лежит на окружности с диаметром \(AC\), то \(\triangle APC\) – прямоугольный, тогда \[\angle CAP = 90^\circ - \angle ACP = \angle ACB - \angle ACP = \angle QCB,\] откуда в итоге следует, что \(\angle PMQ = 90^\circ\).

б) Треугольники \(ABC\) и \(MPQ\) подобны так как они оба прямоугольные и \(\angle MQP = \angle ABC\) как вписанные углы, опирающиеся на одну дугу (отсюда следует подобие по двум углам), тогда \[\dfrac{PQ}{AB} = \dfrac{MQ}{BC}.\]

Так как \(CM\) – высота треугольника \(ABC\), а в прямоугольном треугольнике квадрат высоты, проведённой к гипотенузе, равен произведению отрезков гипотенузы, то \(CM^2 = AM\cdot MB = 3\), откуда \(CM = \sqrt{3}\).

По теореме Пифагора \[CB^2 = CM^2 + MB^2,\] откуда \(CB = 2\sqrt{3}\). Покажем, что \(CMQO_2\) – параллелограмм.

\[CM = \sqrt{3} = \dfrac{CB}{2} = O_2C = O_2Q.\]

Кроме того \(CM\perp AB\). Так как равные дуги стягиваются равными хордами, то \(MQ = QB\). Так как \(O_2M\) и \(O_2B\) – радиусы одной окружности, то \(O_2M = O_2B\).

Таким образом, треугольники \(QMO_2\) и \(QBO_2\) равны по трём сторонам (\(QO_2\) – общая), откуда следует, что \(\angle MQO_2 = \angle BQO_2\), то есть \(QO_2\) содержит биссектрису угла \(MQB\), откуда следует, что \(QO_2\perp MB\) (так как в равнобедренном треугольнике биссектриса, проведённая к основанию, является высотой).

В итоге \(CM\perp AB\perp QO_2\), следовательно, \(CM\parallel QO_2\), но \(CM = QO_2\), откуда следует, что \(CMQO_2\) – параллелограмм. Тогда \(CO_2 = MQ\), следовательно, \[\dfrac{PQ}{AB} = \dfrac{MQ}{BC} = \dfrac{1}{2},\] то есть \(\dfrac{PQ}{4} = \dfrac{1}{2}\), тогда \(PQ = 2\).

Ответ:

б) \(2\)