Задачи с окружностями (страница 3)

Предположим, что прямая \(MN\) пересекает вторую дугу в точке \(P\) и \(P\) – не середина этой дуги. Отметим точку \(P'\) – середину дуги \(\buildrel\smile\over{AB}\).

Рассмотрим \(\triangle MO_1N\) и \(\triangle P'ON\). Они равнобедренные, т.к. \(O_1M=O_1N\) – радиусы окружности \(S_1\), \(OP'=ON\) – радиусы окружности \(S\).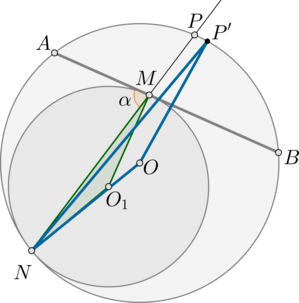

Рассмотрим окружность \(S_1\). Т.к. угол между касательной и хордой, проходящей через точку касания, равен половине дуги, заключенной между ними, то угол между касательной \(AB\) и хордой \(MN\) равен половине дуги \(\buildrel\smile\over{MN}\) (которая меньше полуокружности по рисунку). Обозначим \(\angle AMN=\alpha\). Следовательно, \(\angle MO_1N=2\alpha\), т.к. он центральный, опирающийся на дугу \(\buildrel\smile\over{MM}\), равную \(2\alpha\).

Рассмотрим окружность \(S\). Т.к. \(P'\) – середина дуги \(AB\), то \(\angle AOP'=\angle BOP'\). Следовательно, в равнобедренном треугольнике \(AOB\) \(OP'\) – биссектриса. Следовательно, она и высота, то есть \(OP'\perp AB\). Но \(O_1M\perp AB\) (как радиус, проведенный в точку касания в окружности \(S_1\)), следовательно, обе прямые \(O_1M\) и \(OP'\) перпендикулярны \(AB\), следовательно, они параллельны.
Заметим, что т.к. окружности \(S\) и \(S_1\) касаются, то их центры \(O\) и \(O_1\) и точка касания \(N\) лежат на одной прямой.

Таким образом, \(\angle NO_1M=\angle NOP'=2\alpha\) как соответственные углы при \(O_1M\parallel OP'\) и \(NO\) – секущей.

Значит, \(\angle MNO_1=\frac12\left(180^\circ-2\alpha\right)=\angle P'NO\). А т.к. точки \(N, O_1, O\) лежат на одной прямой, то и точки \(N, M, P'\) лежат на одной прямой. Следовательно, \(P'\) совпадает с \(P\).

Ответ:

Доказательство

а) Рассмотрим треугольники \(AA_1C\) и \(BB_1C\): \(\angle BCA\) – общий, \(\angle AA_1C = 90^\circ = \angle BB_1C\), тогда треугольники \(AA_1C\) и \(BB_1C\) подобны по двум углам.

Из подобия треугольников \(AA_1C\) и \(BB_1C\): \[\dfrac{A_1C}{B_1C} = \dfrac{AC}{BC}\qquad\Leftrightarrow\qquad \dfrac{A_1C}{AC} = \dfrac{B_1C}{BC}.\]

Рассмотрим треугольники \(A_1B_1C\) и \(ABC\): \[\dfrac{A_1C}{AC} = \dfrac{B_1C}{BC},\qquad\qquad \angle ACB\ \text{— общий},\] тогда треугольники \(A_1B_1C\) и \(ABC\) подобны (по пропорциональности сторон и равенству углов между ними).

б) Построим к описанной около \(ABC\) окружности касательную \(l\), проходящую через точку \(C\). Из подобия треугольников \(A_1B_1C\) и \(ABC\): \(\angle BAC = \angle B_1A_1C\).

По теореме об угле между касательной и хордой, угол между прямыми \(l\) и \(BC\) равен половине меньшей из дуг \(BC\), но \(\angle BAC\) – вписанный угол, опирающийся на ту же дугу, тогда \(\angle BAC\) тоже равен половине меньшей из дуг \(BC\), следовательно, \[\angle (BC; l) = \angle BAC = \angle B_1A_1C,\] но \(\angle (BC; l)\) и \(\angle B_1A_1C\) – внутренние накрест лежащие при прямых \(A_1B_1\), \(l\) и секущей \(A_1C\), откуда \(l\parallel A_1B_1\).

Так как \(l\) – касательная к окружности в точке \(C\), то \(OC\perp l\), но \(l\parallel A_1B_1\), тогда \(OC\perp A_1B_1\), следовательно, угол между \(OC\) и \(A_1B_1\) равен \(90^\circ\).

Ответ:

б) \(90^\circ\).

а) Пусть \(AM = a\), \(BN = b\).
Достаточно доказать, что треугольник, составленный из отрезков \(AM\), \(BN\) и \(MN\) – прямоугольный с гипотенузой \(MN\), для этого достаточно доказать, что \[a^2 + b^2 = MN^2\qquad\Leftarrow\qquad a^2 + b^2 = MC^2 + CN^2\qquad\Leftarrow\qquad a^2 + b^2 = (AC - a)^2 + (BC - b)^2,\] следовательно, достаточно доказать, что \[0 = AC^2 - 2\cdot a\cdot AC + BC^2 - 2\cdot b\cdot BC\qquad\Leftarrow\qquad AB^2 = 2\cdot (a\cdot AC + b\cdot BC).\]

Окончательно, таким образом, достаточно доказать, что \[AK^2 + BK^2 = a\cdot AC + b\cdot BC.\] Докажем это.

Так как \(\angle MKN + \angle MCN = 180^\circ\), то в четырёхугольнике \(MKNC\) суммы противоположных углов равны \(180^\circ\), следовательно, около него можно описать окружность.

Пусть множество точек пересечения описанной около \(MKNC\) окружности с \(AB\) есть \(\{K, K'\}\) (т. е., возможно, \(K'\) и \(K\) совпадают, но для дальнейшего решения это не важно).

По теореме о секущих \[AK'\cdot AK = a\cdot AC,\qquad\qquad BK\cdot BK' = b\cdot BC,\] тогда \[AK'\cdot AK + BK\cdot BK' = a\cdot AC + b\cdot BC.\]

С другой стороны, так как \(AK = BK\), то \(KK'\cdot AK = KK'\cdot BK\), откуда \[(AK - AK')\cdot AK = (BK' - BK)\cdot BK\qquad\Rightarrow\qquad AK^2 + BK^2 = AK'\cdot AK + BK\cdot BK'.\]

Получили, что \[AK^2 + BK^2 = AK'\cdot AK + BK\cdot BK' = a\cdot AC + b\cdot BC,\] откуда в итоге следует, что площадь треугольника, составленного из отрезков \(AM\), \(BN\) и \(MN\), равна \[0,5\cdot AM\cdot BN.\]

б) Покажем, что \(MCNK\) – квадрат. Опустим из точки \(K\) на \(BC\) перпендикуляр \(KP\). Из равнобедренности \(ABC\) и подобия треугольников \(KBP\) и \(ABC\) следует, что \(KP = CP\). Обозначим \(NP = y\), тогда \[KN^2 = KP^2 + y^2,\qquad\qquad CN = CP\pm y,\] но \(KN = CN\), тогда \[KP^2 + y^2 = CP^2 + y^2 \pm 2y\cdot CP\qquad\Rightarrow\qquad y\cdot CP = 0,\] следовательно, \(y = 0\) и точки \(N\) и \(P\) совпадают.

Итак, в четырёхугольнике \(MCNK\) три угла равны по \(90^\circ\), следовательно, все его углы равны \(90^\circ\), тогда \(MCNK\) – прямоугольник, но у него соседние стороны равны, тогда \(MCNK\) – квадрат. \(S_{MCNK} = x^2\).

Ответ:

б) \(x^2\).

Заметим, что \(CP\) – диаметр, а \(\angle CBP=90^\circ\) как опирающийся на диаметр.

По условию \(SN=180, OC=60, AB=25\). Пусть также \(BL\) – биссектриса угла \(B\).

Обозначим \(\angle CBL=\angle ABL=\alpha\). Т.к. угол между касательной и хордой, проходящей через точку касания, равен половине дуги, заключенной между ними, то \(\angle CBL=\frac12 \buildrel\smile\over{BC}=\angle CPB=\alpha\).

Т.к. \(SK\parallel PB, SN\parallel PC \quad \Rightarrow \quad \angle KSN=\angle BPC=\alpha\).

\(SO\) — биссектриса угла \(\angle KSN\), следовательно, \(\angle OSN=\frac12 \alpha\). Тогда из \(\triangle OSN\):

\[\mathrm{tg}\,\frac12\alpha=\dfrac{ON}{SN}=\dfrac{60}{180}=\dfrac13\]

Тогда \(\mathrm{tg}\,\alpha= \dfrac{2\mathrm{tg}\,(\frac12\alpha)}{1-\mathrm{tg}^2(\frac12\alpha)}=\dfrac34\).

Следовательно, \(\sin \alpha=\dfrac35, \ \cos\alpha=\dfrac45\). Следовательно

\[\sin \alpha=\dfrac{BC}{PC}=\dfrac{BC}{120} \quad \Rightarrow \quad BC=72\]

Найдем \(AC\) из \(\triangle ABC\) по теореме косинусов: для этого нужно найти \(\cos \angle ABC=\cos 2\alpha\).

\(\cos2\alpha=2\cos^2\alpha-1=2\cdot \left(\dfrac45\right)^2-1=\dfrac7{25}\).

Значит, \(AC^2=AB^2+BC^2-2\cdot AB\cdot BC\cdot \cos2\alpha=4801\).

Ответ: 4801

а) Так как трапеция вписана в окружность, то \(\angle B+\angle D=180^\circ\). Но по свойству трапеции \(\angle B+\angle A=180^\circ\), откуда \(\angle A=\angle D\). Следовательно, трапеция равнобедренная.



Также \(AO=OD=BO=OC\) как радиусы описанной окружности, откуда следует, что точка \(O\) равноудалена от концов отрезка \(AD\) и концов отрезка \(BC\), то есть лежит на серединных перпендикулярах к отрезкам \(AD\) и \(BC\) (на самом деле серединные перпендикуляры к основаниям данной трапеции совпадают, так как к двум параллельным прямым из точки можно провести ровно одну прямую, перпендикулярную этим прямым).

Так как в трапецию вписана окружность, то ее центр \(Q\) лежит на пересечении биссектрис углов трапеции. Следовательно, \(\angle QAD=0,5\angle A=0,5\angle D=\angle QDA\), откуда \(\triangle AQD\) равнобедренный, следовательно, \(Q\) лежит на серединном перпендикуляре к \(AD\).

Чтд.

б)

Как говорилось в пункте а), если около трапеции описана окружность, то трапеция является равнобедренной. Если в трапецию вписана окружность, то сумма оснований трапеции равна сумме боковых сторон. Так как боковые стороны данной трапеции равны, то \(AD+BC=2AB\).
Обозначим \(AB=CD=t\).
Рассмотрим \(\triangle ACD\). Так как около него описана окружность радиуса \(R\), то можно записать теорему синусов: \[\dfrac{CD}{\sin \angle CAD}=2R\] Если \(\cos \angle CAD=\frac34\), то \(\sin\angle CAD=\frac{\sqrt7}4\). Следовательно, \[\dfrac{t}{\frac{\sqrt7}4}=2R\quad\Rightarrow\quad t=\dfrac{\sqrt7}2R\qquad (1)\] Проведем \(CH\perp AD\). По свойству трапеции, в которую вписана окружность, высота трапеции равна \(2r\). Следовательно, \(CH=2r\). Тогда из прямоугольного \(\triangle CAH\): \[\cos \angle CAH=\dfrac{AH}{AC}, \qquad \sin \angle CAH=\dfrac{2r}{AC}\] Отсюда \[AH\cdot \sin\angle CAH=2r\cdot \cos\angle CAH \qquad (*)\] Заметим, что \(HD=0,5(AD-BC)\), следовательно, \(AH=AD-0,5(AD-BC)=0,5(AD+BC)=AB=t\). Тогда из (*) \[t\cdot \dfrac{\sqrt7}4=2r\cdot \dfrac34\quad\Rightarrow\quad t=\dfrac{6r}{\sqrt7} \qquad (2)\] Тогда из (1) и (2) равенств получаем: \[r=\dfrac{7R}{12}=7\]

Ответ:

б) 7

а) Если в четырехугольник можно вписать окружность, то суммы противоположных сторон четырехугольника должны быть равны. Найдем все стороны трапеции \(ABCD\).

Так как \(\angle BAC=\angle CDB\), то четырехугольник \(ABCD\) является вписанным в окружность. Следовательно, \(\angle ABD=\angle ACD\) как вписанные углы, опирающиеся на дугу \(AD\). Обозначим \(\angle BAC=\alpha\), \(\angle ABD=\beta\). Тогда по свойству угол между секущими равен полуразности дуг, заключенных между ними: \(\angle AKD=0,5\cdot (2\beta-2\alpha)\).
Но в то же время \(\alpha+\beta=90^\circ\) из прямоугольного \(\triangle ABO\) (\(O\) – точка пересечения диагоналей трапеции).

Получаем: \[\begin{cases} 30^\circ=\beta-\alpha\\[2ex] \alpha+\beta=90^\circ\end{cases} \quad\Rightarrow\quad \begin{cases} \alpha=30^\circ \\ \beta=60^\circ\end{cases}\]

Пусть \(BO=x\). Тогда из прямоугольного \(\triangle ABO\), так как \(\angle BAO=30^\circ\), следует, что \(AB=2x\). По теореме Пифагора \(AO=\sqrt3 x\).
Так как трапеция вписана в окружность, то она равнобедренная, значит, ее диагонали равны, а также \(BO=CO\) и \(AO=DO\). Тогда \(CO=x\), \(DO=\sqrt 3x\), следовательно, \(BC=x\cdot \sqrt2\), \(AD=\sqrt3 x\cdot \sqrt2\).
Проверка: \[AD+BC=AB+CD\quad\Rightarrow\quad \sqrt6 x+\sqrt2 x=4x \quad\Rightarrow\quad \sqrt 6+\sqrt 2=4\] Полученное равенство неверно, следовательно, в трапецию вписать окружность нельзя.

б) Из того, что \(\angle BAO=\angle CDO=\angle K=30^\circ\), следует, что \(\triangle AKC\) и \(\triangle DBK\) равнобедренные, откуда \(AC=CK\) и \(DB=BK\).

Как известно, площадь выпуклого четырехугольника равна полупроизведению диагоналей на синус угла между ними. Следовательно, если диагонали взаимно перпендикулярны, то площадь равна полупроизведению диагоналей: \[S_{ABCD}=\dfrac12\cdot AC\cdot DB\] Следовательно, получаем: \[60=\dfrac12\cdot CK\cdot BK\quad\Rightarrow\quad CK\cdot BK=120\]

Так как площадь треугольника равна полупроизведению сторон на синус угла между ними, то \[S_{BKC}=\dfrac12\cdot CK\cdot BK\cdot \sin 30^\circ= \dfrac12\cdot 120\cdot \dfrac12=30\]

Следовательно, \[S_{AKD}=60+30=90\]

Ответ:

б) 90

а) Обозначим вершины треугольника \(T\) через \(A'\), \(B'\) и \(C'\) как показано на рисунке. Пусть \(O\) – центр треугольника \(ABC\).

Так как своими центром и радиусом любая окружность определяется однозначно, то точки \(A'\), \(B'\) и \(C'\) однозначно определяются положениями точек \(A\), \(B\) и \(C\) и числом \(R\).

Так как поворот плоскости является движением (сохраняет любые расстояния), то при повороте плоскости на \(120^\circ\) вокруг точки \(O\) множество точек \(\{A; B; C\}\) перейдёт само в себя, следовательно, и множество точек \(\{A'; B'; C'\}\) перейдёт само в себя.

Если бы одна из сторон треугольника \(T\) была длиннее других его сторон, то при повороте плоскости множество \(\{A'; B'; C'\}\) не перешло бы в себя (иначе длинная сторона перешла бы в более короткую, но поворот плоскости – движение), следовательно, у \(T\) нет стороны, которая длиннее других, следовательно, \(T\) – равносторонний, а все равносторонние треугольники подобны.

б) Рассмотрим треугольник \(AC'B\): \(AC' = C'B = R\), \(AB = a\).

Этими данными треугольник определяется однозначно. Обозначим \(\angle C'AB = \alpha\) и запишем для него теорему косинусов: \[R^2 = R^2 + a^2 - 2aR\cos\alpha\qquad\Leftrightarrow\qquad\cos\alpha = \dfrac{a}{2R}\]

\(\angle CAB' = \alpha\) так как треугольники \(ABC'\) и \(AB'C\) равны по трём сторонам, тогда \(\angle C'AB = 2\alpha + 60^\circ\).

По теореме косинусов в треугольнике \(C'AB'\):

\[\begin{aligned} &{C'B'}^2 = R^2 + R^2 - 2R^2\cos(2\alpha + 60^\circ)\ \Rightarrow\ {C'B'}^2 = 2R^2 - 2R^2(\cos(2\alpha)\cdot\cos 60^\circ - \sin(2\alpha)\cdot\sin 60^\circ) =\\ &= 2R^2 - 2R^2\left((2\cos^2\alpha - 1)\cdot 0,5 - 2\sin\alpha\cos\alpha\cdot\dfrac{\sqrt{3}}{2}\right) \end{aligned}\]

Из основного тригонометрического тождества при учёте того, что \(0\leq\alpha < 180^\circ\): \[\sin\alpha = \sqrt{1 - \cos^2\alpha} = \sqrt{1 - \dfrac{a^2}{4R^2}}.\]

Итого

\[\begin{aligned} &{C'B'}^2 = 2R^2 - 2R^2\left(\left(\dfrac{a^2}{2R^2} - 1\right)\cdot 0,5 - \sqrt{1 - \dfrac{a^2}{4R^2}}\cdot\dfrac{a}{2R}\cdot\sqrt{3}\right) = 3R^2 - 0,5a^2 + \dfrac{\sqrt{3}}{2}a\sqrt{4R^2 - a^2}\\ &\Rightarrow\qquad C'B' = \sqrt{3R^2 - 0,5a^2 + \dfrac{\sqrt{3}}{2}a\sqrt{4R^2 - a^2}}, \end{aligned}\]

следовательно, периметр \(T\) равен \[3\sqrt{3R^2 - 0,5a^2 + \dfrac{\sqrt{3}}{2}a\sqrt{4R^2 - a^2}}\,.\]

Ответ:

б) \(3\sqrt{3R^2 - 0,5a^2 + \dfrac{\sqrt{3}}{2}a\sqrt{4R^2 - a^2}}\)