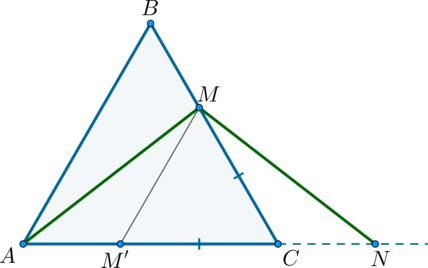
Диагонали \(AC\) и \(BD\) трапеции \(ABCD\) (\(AD\parallel BC\)) взаимно перпендикулярны, длина средней линии трапеции равна \(m\). На большем основании \(AD\) взята точка \(M\) так, что \(AM=m\). Найдите длину отрезка \(MC\).
Пусть \(BC=2a\), \(AD=2b\). Тогда \(m=a+b\). Тогда \(MD=AD-AM=2b-a-b=b-a\). Соединим середины оснований и получим отрезок \(NK\). По свойству трапеции этот отрезок проходит через точку пересечения диагоналей. Тогда \(KM=AM-AK=a+b-b=a\). Следовательно, \(KNCM\) – параллелограмм (две стороны \(KM\) и \(NC\) равны \(a\) и параллельны). Таким образом, \(NK=CM\). Значит, найдем \(NK\).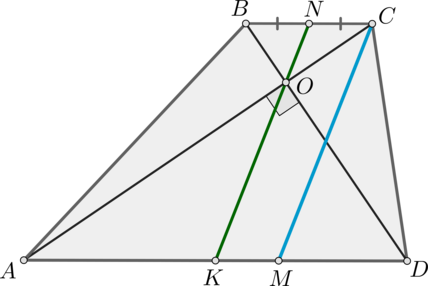
\(ON\) и \(OK\) – медианы в прямоугольных треугольниках \(BOC\) и \(AOD\) соответственно, проведенные к гипотенузе. Следовательно, каждая из них равна половине гипотенузы, то есть \(ON=a\), \(OK=b\). Тогда \(NK=a+b=m\). Следовательно, и \(CM=m\).
Ответ:
\(m\)