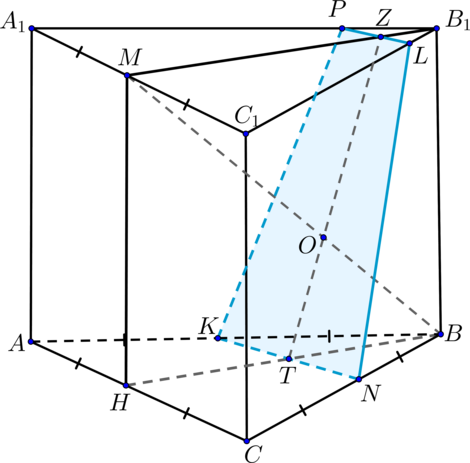
а) Рассмотрим четырехугольник \(MNKL\). Т.к. плоскости основания параллельны, то линии пересечения этих плоскостей с плоскостью \(MNK\) тоже параллельны, то есть \(NK\parallel ML\).
Заметим, что если совместить наложением равные равносторонние треугольники \(ABC\) и \(A_1B_1C_1\) так, чтобы точка \(B_1\) наложилась на \(A\), точка \(N\) на \(M\), то точка \(K\) наложится на \(L\) (из-за параллельности \(NK\) и \(ML\)).
Следовательно, \(\triangle AML=\triangle B_1NK\). Следовательно, \(ML=NK\). Таким образом, по признаку \(MNKL\) – параллелограмм.
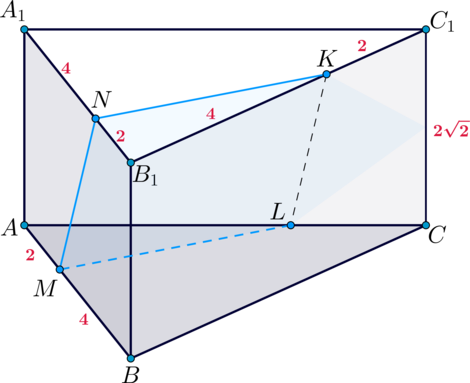
Как следствие, \(AL=B_1K=4\).
По теореме косинусов из \(\triangle AML\) найдем \[ML^2=2^2+4^2-2\cdot 2\cdot 4\cdot \cos60^\circ=12
\quad \Rightarrow \quad ML=2\sqrt3.\]
Заметим, что \(AL^2=AM^2+ML^2\) (\(4^2=2^2+(2\sqrt3)^2\)), следовательно, по обратной теореме Пифагора \(\angle AML=90^\circ\).
Таким образом, \(ML\perp AB\) и \(ML\perp BB_1\), следовательно, \(ML\perp (ABB_1)\), следовательно, \(ML\perp MN\).
Таким образом, \(\angle NML=90^\circ\) и \(MNKL\) – параллелограмм, у которого один угол прямой, следовательно, все углы прямые, следовательно, это прямоугольник.
Для того, чтобы доказать, что это квадрат, достаточно доказать равенство двух смежных сторон. Поэтому покажем, что \(ML=MN\).
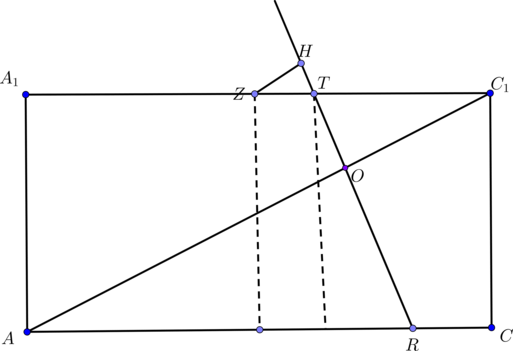
Рассмотрим грань \(ABB_1A_1\) и проведем в ней \(NN_1\perp AB\), чтобы найти \(MN\).
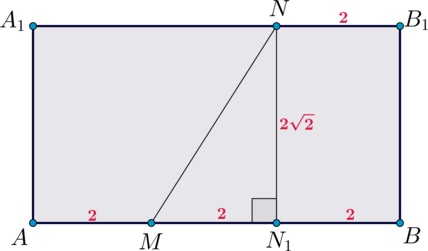
Тогда \(N_1B=NB_1=2\), следовательно, \(MN_1=6-2-2=2\). Тогда из прямоугольного \(\triangle MNN_1\) имеем:
\[MN=\sqrt{2^2+(2\sqrt2)^2}=2\sqrt3.\]
Таким образом, \(MN=ML\), чтд.
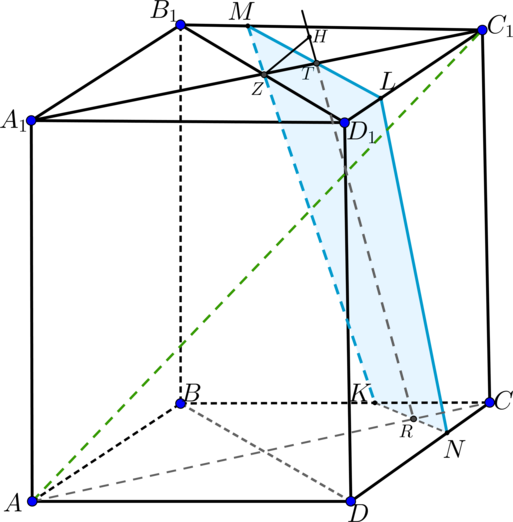
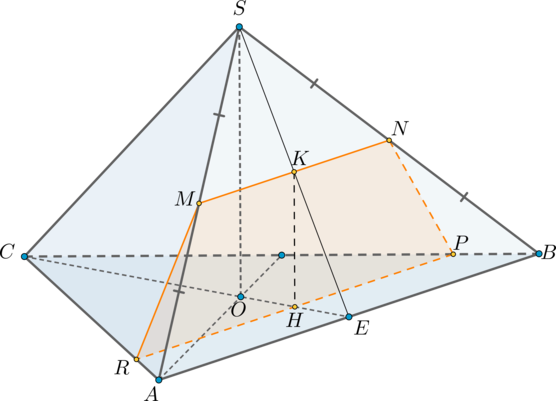
б) Построим сечение призмы плоскостью \(MNK\). Для этого необходимо найти отрезки, по которым она пересекает грани \(BB_1C_1C\) и \(ACC_1A_1\).
Пусть \(O\) – точка пересечения прямых \(ML\) и \(BC\). Тогда \(O\) лежит в грани \(BCC_1B_1\). Следовательно, соединив точки \(O\) и \(K\), получим точку пересечения плоскости с ребром \(CC_1\) – точку \(P\). Тогда \(MNKPL\) – искомое сечение.
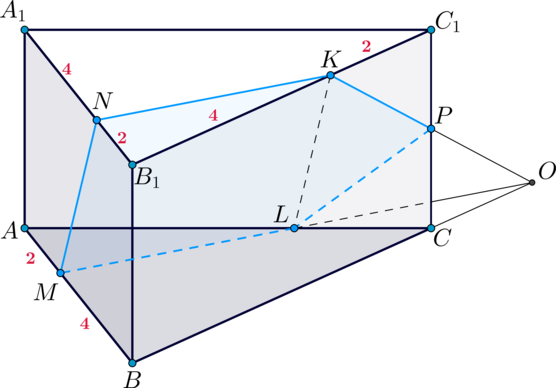
Его площадь будем искать как сумму площади квадрата \(MNKL\) и треугольника \(KPL\).
Площадь квадрата \(MNKL\) равна \((2\sqrt3)^2=12\).
По теореме Менелая для \(\triangle ABC\) и прямой \(MO\) имеем:
\[\dfrac{BM}{MA}\cdot \dfrac{AL}{LC}\cdot \dfrac{CO}{OB}=1
\quad \Rightarrow \quad \dfrac42\cdot \dfrac42\cdot \dfrac{CO}{OB}=1
\quad \Rightarrow \quad CO=2.\]
Таким образом, \(\triangle PKC_1=\triangle POC\) как прямоугольные по катету и острому углу, следовательно, \(CP=PC_1=\sqrt2\).
Тогда по теореме Пифагора:
\[\begin{aligned}
&KP=\sqrt{2^2+(\sqrt2)^2}=\sqrt6;\\
&LP=\sqrt{2^2+(\sqrt2)^2}=\sqrt6 \end{aligned}\]
То есть \(\triangle KPL\) равнобедренный. Следовательно, его высота \(h\) из вершины \(P\) к основанию (на рисунке не отмечена) по теореме Пифагора ищется как \[h=\sqrt{(\sqrt6)^2-(\sqrt3)^2}=\sqrt3.\]
Тогда \[S_{\triangle KPL}=\dfrac12\cdot \sqrt3\cdot 2\sqrt3=3\]
Следовательно, площадь сечения равна \(12+3=15\).
Ответ:
\(15\)