1. Квадратичное неравенство \(ax^2+bx+c> 0\). Если уравнение \(ax^2+bx+c=0\) имеет корни \(x_1, x_2\) (или один корень \(x_1\)), его можно переписать в виде \(a(x-x_1)(x-x_2)>0\) (\(a(x-x_1)^2>0\)) и далее решить методом интервалов.
Если уравнение не имеет корней, то при \(a>0\) выражение \(ax^2+bx+c>0\), при \(a<0\) выражение \(ax^2+bx+c<0\) при всех \(x\).

2. Показательное неравенство \(a^{f(x)}> a^{g(x)}\) равносильно \(f>g\), если \(a>1\), или \(f<g\), если \(0<a<1\).

3. Логарифмическое неравенство \(\log_a{f(x)}> \log_a{g(x)}\) равносильно \(f>g\), если \(a>1\), или \(f<g\), если \(0<a<1\), при условии выполненного ОДЗ: \(f>0, g>0\).

Задание 29 #1340

Уровень задания: Сложнее ЕГЭ

Азат толкнул ядро под углом \(\phi\) к горизонтальной поверхности земли. Продолжительность полета ядра в секундах можно найти по формуле \[t = \dfrac{2v_0\sin{\phi}}{g}.\] При каком наибольшем значении угла \(\phi\) в градусах время полета ядра будет не менее, чем \(1,2\) секунды, если Азат толкнул его с начальной скоростью \(v_0 = 12\) м/с? Считайте, что ускорение свободного падения \(g = 10\) м/с\(^2\).

Показать решение

\[1,2 \leq t = \dfrac{2\cdot 12\cdot \sin \phi}{10} \qquad\Leftrightarrow\qquad\sin \phi \geq 0,5.\] Решим неравенство \(\sin \phi \geq 0,5\) методом интервалов. Найдем корни уравнения \(\sin \phi = 0,5\): \[\phi = \dfrac{\pi}{6} + \pi k,\qquad\qquad \phi = \dfrac{5\pi}{6} + \pi k,\] где \(k \in \mathbb{Z}\). Тогда: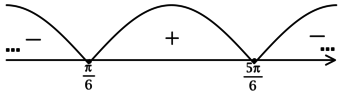

здесь бесконечно много интервалов, но знаки в них чередуются. Кроме того, \(\phi \in [0; \pi)\), тогда: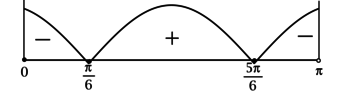

тогда \(\phi \in \left[\dfrac{\pi}{6}; \dfrac{5\pi}{6}\right]\) и наибольшее подходящее значение \(\phi\) равно \(\dfrac{5\pi}{6}\), то есть \(150^{\circ}\).

Ответ: 150

Задание 30 #1332

Уровень задания: Сложнее ЕГЭ

Маша подбросила мячик, высота которого до падения меняется по закону \(h = 1 + 7t - 5t^2\), где \(h\) – высота в метрах, \(t\) – время в секундах, отсчитываемое от момента подбрасывания. Сколько секунд с момента подбрасывания мячик находился на высоте не менее \(1\) метра, но не более \(2,2\) метров?

Показать решение

Моменты \(t\), в которые мячик находился на высоте не менее \(1\) метра, но не более \(2,2\) метров удовлетворяют двойному неравенству \[1 \leq 1 + 7t - 5t^2 \leq 2,2.\] Решим два неравенства по очереди.

Рассмотрим неравенство \(1 \leq 1 + 7t - 5t^2\). Оно равносильно неравенству \[5t^2 - 7t \leq 0,\] которое решим методом интервалов. Найдём корни уравнения \(5t^2 - 7t = 0\): \[t_1 = 0, \qquad\qquad t_2 = 1,4,\] тогда:

тогда решениями этого неравенства будут \(t\in[0; 1,4]\).

Рассмотрим теперь неравенство \(1 + 7t - 5t^2 \leq 2,2\). Оно равносильно неравенству \[5t^2 -7t + 1,2 \geq 0,\] которое решим методом интервалов. Найдём корни уравнения \(5t^2 -7t + 1,2 = 0\): \[t_1 = 0,2, \qquad\qquad t_2 = 1,2,\] тогда:

но с учётом того, что \(t \geq 0\) подходят только \(t\in[0; 0,2] \cup [1,2; +\infty)\).

В итоге мячик находился на высоте не менее \(1\) метра, но не более \(2,2\) метров в моменты \(t\in[0; 0,2] \cup [1,2; 1,4]\), то есть в течение \((0,2 - 0) + (1,4 - 1,2) = 0,4\) секунды.

Ответ: 0,4

Задание 31 #1331

Уровень задания: Сложнее ЕГЭ

Подводная лодка “Скумбрия”\(\ \)плывет с постоянной скоростью \(v_0 = 20\) узлов (1 узел = 1 морская миля в час). В момент времени \(t = 0\) часов она выпускает торпеду, которая до попадания в цель разгоняется с постоянным ускорением \(a = 80\) узлов в час. Расстояние в морских милях от места пуска до торпеды определяется из формулы \[S = v_0t+\dfrac{at^2}{2}.\] Определите в течение какого времени с момента пуска торпеда плыла последние \(1,3\) морской мили до цели, если в момент пуска расстояние до неподвижной цели было 2,4 морских мили. Ответ дайте в часах.

Показать решение

Разделим путь торпеды на 2 участка: участок А – первые 1,1 морской мили пути; участок В – последние 1,3 морской мили пути. Тогда моменты \(t\), в которые торпеда будет находиться на участке В, удовлетворяют двойному неравенству \[1,1 \leq 20t + 40t^2 \leq 2,4.\] Решим два неравенства по очереди.

Рассмотрим неравенство \(1,1 \leq 20t + 40t^2\). Оно равносильно неравенству \[40t^2 + 20t - 1,1 \geq 0,\] которое решим методом интервалов. Найдём корни уравнения \(20t + 40t^2 - 1,1 = 0\): \[t_1 = -0,55,\qquad\qquad t_2 = 0,05,\] тогда:

но с учётом того, что \(t \geq 0\) подходят только \(t \geq 0,05\).

Рассмотрим теперь неравенство \(20t + 40t^2 \leq 2,4\). Оно равносильно неравенству \[40t^2 + 20t - 2,4 \leq 0,\] которое решим методом интервалов. Найдём корни уравнения \(20t + 40t^2 - 2,4 = 0\): \[t_1 = -0,6,\qquad\qquad t_2 = 0,1,\] тогда:

но с учётом того, что \(t \geq 0\) подходят только \(0 \leq t \leq 0,1\).

В итоге торпеда находилась на участке В в моменты \(0,05 \leq t \leq 0,1\), то есть в течение \(0,1 - 0,05 = 0,05\) часа.

Ответ: 0,05

Задание 32 #4024

Уровень задания: Легче ЕГЭ

Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: \[T(t)=T_0+bt+at^2,\]где \(t\) – время в минутах, \(T_0=1300\) К, \(a=-\dfrac{14}3\) К/мин\(^2\), \(b=98\) К/мин.
Известно, что при температуре нагревательного элемента свыше \(1720\) К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

Показать решение

Из условия задачи следует, что \(T(t)\) должно быть не больше \(1720\), то есть, подставляя все данные из условия, получим следующее неравенство \[1300+98t-\dfrac{14}3t^2\leqslant 1720 \ \Big|\cdot \left(-\dfrac3{14}\right) \quad\Leftrightarrow\quad t^2-21t+90\geqslant 0\] Корнями многочлена \(t^2-21t+90\) являются \(t=6\) и \(t=15\). Следовательно, решением неравенства будут \(t\in (-\infty;6]\cup[15;+\infty)\).

Таким образом, наибольшее время, после которого нужно отключить прибор, равно \(6\) (мин).
Из решения неравенства следует, что после 6-ой минуты температура нагревательного элемента превысит 1720 К, то есть после 6-ой минуты нагревательный элемент уже испортился ! Именно поэтому мы выбираем ответ 6 минут.

Ответ: 6

1 ... 4 5