Задачи с параметром из ЕГЭ прошлых лет (страница 4)

Преобразуем скобку в числителе дроби: \[y^2-xy+3x-y-6=0 \quad\Leftrightarrow\quad y^2-(x+1)y+3x-6=0\] Дискриминант равен \(D=(x-5)^2\quad\Rightarrow\) \[y_1=\dfrac{x+1+x-5}2=x-2\quad\text{и}\quad y_2=\dfrac{x+1-x+5}2=3.\] Таким образом, всю систему можно записать в виде: \[\begin{cases} \left[\begin{gathered}\begin{aligned} &y^2-(x+1)y+3x-6=0\\ &x+2=0\end{aligned}\end{gathered} \right.\\ 6-x>0\\ x+2\geqslant 0\\ y=-x+a\end{cases} \quad\Leftrightarrow\quad \begin{cases} \left[\begin{gathered}\begin{aligned} &y=x-2\\ &y=3\\ &x=-2\end{aligned}\end{gathered} \right.\\ -2\leqslant x<6\\ y=-x+a\end{cases}\]

Найдем значения параметра, при каждом из которых прямая \(y=-x+a\) имеет две точки пересечения с графиком системы \(\begin{cases} \left[\begin{gathered}\begin{aligned} &y=x-2\\ &y=3\\ &x=-2\end{aligned}\end{gathered} \right.\\ -2\leqslant x<6\end{cases}\)  

Рассмотрим рисунок: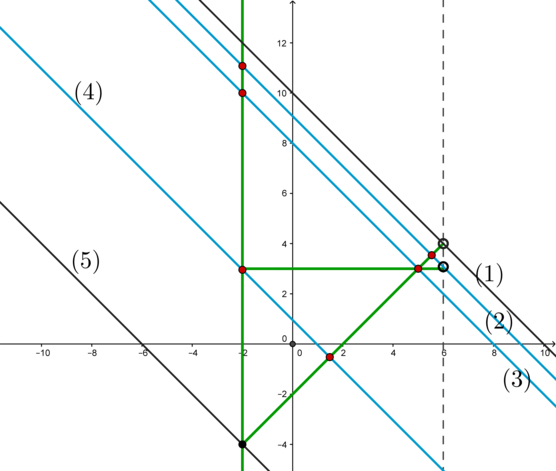

Зеленым цветом изображен график системы, синим и черным – возможные положения прямой \(y=-x+a\).

1) Заметим, что если прямая \(y=-x+a\) находится в положении (1) (проходит через точку \((6;4)\) пересечения \(y=x-2\) и \(x=6\)) и выше, то она имеет только одну точку пересечения с графиком системы.
Между положениями (1) и (2) и в положении (2) (проходит через точку \((6;3)\) пересечения \(y=3\) и \(x=6\)) прямая \(y=-x+a\) имеет две точки пересечения с графиком системы. Найдем соответствующие значения параметра.

Положение (1): \(a=10\);
положение (2): \(a=9\).

Следовательно, при \(a\in[9;10)\) имеем две точки пересечения.

2) Между положениями (2) и (3) – три точки пересечения, а вот в положении (3) (проходит через точку \((5;3)\) пересечения \(y=3\) и \(y=x-2\)) – две точки.
Положение (3): \(a=8\).

3) Между положениями (3) и (4) – три точки пересечения, а вот в положении (4) (проходит через точку \((-2;3)\) пересечения \(y=3\) и \(x=-2\)) – две точки.
Положение (4): \(a=1\).

4) Между положениями (4) и (5) – две точки пересечения.
Положение (5) – прямая \(y=-x+a\) проходит через точку \((-2;-4)\) пересечения \(x=-2\) и \(y=x-2\), следовательно, \(a=-6\).

Следовательно, при \(a\in (-6;1)\) имеем две точки пересечения.

Собрав все подходящие значения параметра, получим: \(a\in (-6;1]\cup\{8\}\cup[9;10)\).

Ответ:

\(a\in (-6;1]\cup\{8\}\cup[9;10)\)

Сделаем замену: \(\sin x+1=t\), следовательно, \(t\in [0;2]\). Тогда неравенство примет вид: \[|3t+a^2-25|+|7t+a+5|\leqslant 11t+|a^2+a-20|\] Заметим, что при раскрытии модулей в левой части (на соответствующем промежутке) коэффициент перед \(t\) (в левой части) будет равен либо \(7+3=10\), либо \(7-3=4\), либо \(3-7=-4\), либо \(-3-7=-10\). В любом случае при переносе данного слагаемого в правую часть и приведении подобных слагаемых коэффициент перед \(t\) (в правой части) будет положительным.
Например, если модули раскроются оба положительными (то есть \(3t>-a^2+25, \ 7t>-a-5\)), то неравенство для таких \(t\) примет вид: \[3t+a^2-25+7t+a+5\leqslant 11t+|a^2+a-20|\quad\Leftrightarrow\quad 0\leqslant t+|a^2+a-20|-a^2-a+20\quad\Leftrightarrow\quad t+|a^2+a-20|-a^2-a+20\geqslant0\] Следовательно, справа получается возрастающая линейная функция.

Таким образом, можно сделать вывод, что как бы ни раскрылись модули, функция \(y(t)=11t+|a^2+a-20|-|3t+a^2-25|-|7t+a+5|\) всегда будет монотонно возрастающей.
Поэтому если рассмотреть неравенство в виде \[y(t)=11t+|a^2+a-20|-|3t+a^2-25|-|7t+a+5|\geqslant 0,\] то для того, чтобы неравенство при всех \(t\in[0;2]\) выполнялось, достаточно, чтобы график возрастающей функции \(y(t)\) был выше оси \(Ox\). Следовательно, значение \(y(0)\) (в левой точке отрезка \([0;2]\)) должно быть неотрицательным:

\[11\cdot 0+|a^2+a-20|-|3\cdot 0+a^2-25|-|7\cdot 0+a+5|\geqslant 0 \quad\Leftrightarrow\quad |a^2+a-20|\geqslant|a^2-25|+|a+5|\] Заметим, что \(a^2-25+a+5=a^2+a-20\). Следовательно, данное неравенство имеет вид: \(|A+B|\geqslant |A|+|B|\). Как известно, при всех \(A\) и \(B\) выполняется неравенство: \(|A+B|\leqslant |A|+|B|\). Следовательно, наше неравенство выполняется тогда и только тогда, когда \[|A+B|=|A|+|B|\] Для того, чтобы модуль суммы был равен сумме модулей двух чисел \(A\) и \(B\), хотя бы одно из них должно быть равно нулю либо они должны быть одного знака, следовательно, данное равенство равносильно \[AB\geqslant 0\quad\Rightarrow\quad (a^2-25)(a+5)\geqslant 0\quad\Rightarrow\quad (a+5)^2(a-5)\geqslant 0\quad\Rightarrow\quad a\in \{-5\}\cup[5;+\infty).\]

Ответ:

\(a\in \{-5\}\cup[5;+\infty)\)

Заметим, что \(\mathrm{tg}\,x\) – периодическая функция с периодом \(\pi\). Таким образом, если данное уравнение будет иметь решение на \(\left[0;\frac{\pi}2\right)\), то оно также будет иметь еще одно решение на \(\left[\pi;\frac{3\pi}2\right)\) (в точках \(\frac{\pi}2, \frac{3\pi}2\) тангенс не определен). А вот решения из промежутка \(\left(\frac{\pi}2;\pi\right)\) не дублируются на отрезке \(\left[0;\dfrac{3\pi}2\right]\).
Таким образом, данное уравнение будет иметь два решения на отрезке \(\left[0;\dfrac{3\pi}2\right]\) в одном из двух случаев:

1) Если оно будет иметь ровно одно, причем неотрицательное, решение относительно \(\mathrm{tg}\,x\).

2) Если оно будет иметь ровно два различных, причем отрицательных, решения относительно \(\mathrm{tg}\,x\).

Рассмотрим первый случай.

Введем обозначение \(\mathrm{tg}\,x+6=t\). Тогда \(t\geqslant 6\). Получим уравнение: \[t^2-(a^2+2a+8)t+a^2(2a+8)=0\]Заметим, что по теореме Виета корнями данного уравнения будут: \[t_1=2a+8\quad\text{и}\quad t_2=a^2\]Для того, чтобы уравнение имело ровно один корень, причем \(t\geqslant 6\), нужно:\[\begin{cases} t_1=t_2\\t_1\geqslant 6\end{cases} \quad\Rightarrow\quad a=4.\]

Рассмотрим второй случай.

Т.к. в этом случае \(\mathrm{tg}\,x<0\quad\Rightarrow\quad t<6\).
Также остается: \[t_1=2a+8\quad\text{и}\quad t_2=a^2\] Для того, чтобы уравнение имело два корня, причем оба были меньше \(6\), нужно:\[\begin{cases} t_1\ne t_2\\t_1<6\\t_2<6\end{cases}\quad\Rightarrow\quad \begin{cases}-\sqrt6<a<-1\\a\ne -2\end{cases}\]

Таким образом, окончательный ответ в задаче: \[a\in (-\sqrt6;-2)\cup(-2;-1)\cup\{4\}.\]

Ответ:

\(a\in(-\sqrt6;-2)\cup(-2;-1)\cup\{4\}\)

1) Сделаем замену: \(x+\frac1{x-a}=t\). Полученное уравнение \[t^2-(a+9)t+2a(9-a)=0\] по теореме Виета имеет два (может быть, совпадающих) корня \[t_1=9-a\quad\text{и}\quad t_2=2a.\] Заметим, что для того, чтобы исходное уравнение имело четыре решения, необходимо, чтобы полученное уравнение относительно \(t\) имело два различных решения. Следовательно, \[9-a\ne 2a\quad\Leftrightarrow\quad a\ne 3\]

2) Сделаем обратную замену: \[\left[\begin{gathered}\begin{aligned} &x+\dfrac1{x-a}=2a\\[2ex] &x+\dfrac1{x-a}=9-a \end{aligned}\end{gathered}\right. \quad\Leftrightarrow\quad\begin{cases}\left[\begin{gathered}\begin{aligned} &x^2-9x-a^2+9a+1=0\\ &x^2-3ax+2a^2+1=0 \end{aligned}\end{gathered}\right.\\x\ne a\end{cases}\]

Следовательно, каждое из двух полученных квадратных уравнений должно иметь два различных корня, не равные \(a\), причем все четыре этих корня должны быть различны.

а) Значит, во-первых, у уравнений должны быть положительные дискриминанты: \[\begin{cases} D_1=4a^2-36a+77>0\\ D_2=a^2-4>0\end{cases} \quad\Leftrightarrow\quad a\in (-\infty;-2)\cup\left(2;\frac72\right)\cup\left(\frac{11}2;+\infty\right)\]

б) Во-вторых, \(x=a\) не должно являться корнем ни одного из двух уравнений, то есть \[\begin{cases} a^2-9a-a^2+9a+1\ne 0\\ a^2-3a^2+2a^2+1\ne 0\end{cases} \quad\Leftrightarrow\quad a\in \mathbb{R}\]

в) В-третьих, ни один корень одного уравнения не должен совпадать ни с одним корнем второго уравнения. Найдем значения \(a\), при которых уравнения имеют одинаковый корень \(x_0\): \[x_0^2-9x_0-a^2+9a+1=x_0^2-3ax_0+2a^2+1\quad\Leftrightarrow\quad (a-3)(x_0-a)=0\] Таким образом, либо \(a\) должно быть равно \(3\) (но это значение параметра мы исключили в 1-ом пункте решения), либо этот общий корень должен быть равен \(a\) (это мы также проверили в б)).

Следовательно, учитывая \(a\ne 3\), получаем окончательный ответ \[a\in (-\infty;-2)\cup(2;3)\cup\left(3;\frac72\right)\cup \left(\frac{11}2;+\infty\right)\]

Ответ:

\(a\in (-\infty;-2)\cup(2;3)\cup\left(3;\frac72\right)\cup\left(\frac{11}2;+\infty\right)\)

1) Сделаем замену \(t=|x+2|+|x-a|\). Тогда уравнение примет вид \[t^2-5t+3a(5-3a)=0.\] Получили квадратное уравнение. Для того, чтобы изначальное уравнение относительно \(x\) имело решения, полученное уравнение относительно \(t\) должно иметь решения, то есть его дискриминант должен быть неотрицательным. Найдем дискриминант: \[D=25-60a+36a^2=(6a-5)^2\geqslant 0.\] Таким образом, дискриминант для любого \(a\) будет неотрицательным. Имеем корни: \[t_1=\dfrac{5+6a-5}2=3a\qquad \text{и}\qquad t_2=\dfrac{5-6a+5}2=5-3a.\]

2) Таким образом, исходное уравнение равносильно совокупности: \[\left[\begin{gathered}\begin{aligned} &|x+2|+|x-a|=3a\\&|x+2|+|x-a|=5-3a \end{aligned}\end{gathered} \right.\] Оба уравнения в данной совокупности имеют вид: \[|x+2|+|x-a|=t,\]где \(t\) – некоторое выражение, зависящее от \(a\). Исследуем такое уравнение.

Заметим, что т.к. модуль всегда неотрицателен, то и сумма двух модулей всегда неотрицательна, то есть слева стоит неотрицательное выражение. Значит, для того, чтобы данное уравнение имело решения, необходимо, чтобы \(t\geqslant 0\). Рассмотрим уравнение в виде: \[|x+2|=t-|x-a|\] Пусть \(y_1=|x+2|, y_2=t-|x-a|\). Тогда график \(y_1\) представляет собой угол с ветвями вверх, вершина которого находится в точке \((-2;0)\), а график \(y_2\) – угол с ветвями вниз, вершина которого находится в точке \((a;t)\) (помним, что \(t\geqslant 0\)).

Тогда уравнение будет иметь два решения (то есть две точки пересечения графиков \(y_1\) и \(y_2\)), если вершина угла \(y_2\) находится внутри угла \(y_2\). Одно решение, если вершины углов совпадут (тогда \(a=-2, t=0\)). Бесконечное множество решений (отрезок), если вершина угла \(y_2\) попадет на одну из ветвей угла \(y_1\). Не будет иметь решений, если вершина угла \(y_2\) будет находиться снаружи угла \(y_1\).

Рассмотрим интересующий нас случай, когда уравнение имеет два решения. Тогда \(a\) должно находиться между числами \(x_2\) и \(x_1\).
Правая ветвь угла \(y_1\) задается уравнением \(y=x+2\), следовательно, \(t=x_1+2\quad \Rightarrow \quad x_1=t-2\).
Левая ветвь задается уравнением \(y=-x-2\), следовательно, \(t=-x_2-2\quad\Rightarrow\quad x_2=-t-2\).

Таким образом, для того, чтобы уравнение имело два решения, необходимо и достаточно:\[\begin{cases} -t-2<a<t-2\\t\geqslant 0\end{cases}\]

3) Заметим, что в нашем случае уравнение не может иметь одно решение, т.к. одновременное выполнение \(a=-2\) и \(t=0\) при \(t=3a\) или \(t=5-3a\) невозможно.

Следовательно, вся совокупность из двух уравнений будет иметь два решения тогда и только тогда, когда первое имеет два решения, а второе – ни одного, или наоборот.

4) Рассмотрим первое уравнение. \[|x+2|=3a-|x-a|\] Оно имеет два решения, когда:\[\begin{cases} -3a-2<a<3a-2\\3a\geqslant 0\end{cases} \quad\Rightarrow\quad a>1\] Тогда оно не имеет решений, когда \(a\leqslant 1\).

Рассмотрим второе уравнение. \[|x+2|=5-3a-|x-a|\] Оно имеет два решения, когда:\[\begin{cases} -5+3a-2<a<5-3a-2\\5-3a\geqslant 0\end{cases}\quad\Rightarrow\quad a<\dfrac34\] Тогда оно не имеет решений, когда \(a\geqslant \frac34\).

5) Таким образом, нужно: \[\left[\begin{gathered}\begin{aligned} &\begin{cases} a>1\\a\geqslant\frac34\end{cases}\\ &\begin{cases} a\leqslant 1\\a<\frac34\end{cases} \end{aligned}\end{gathered}\right. \quad\Rightarrow\quad a\in\left(-\infty;\frac34\right)\cup(1;+\infty).\]

Ответ:

\(\left(-\infty;\frac34\right)\cup(1;+\infty)\)

1) Сделаем замену: \(t=\log_8(x+a)-\log_8(x-a)\), тогда уравнение примет вид \[t^2-12at+35a^2-6a-9=0\] Дискриминант данного уравнения равен \[D=4(a+3)^2\geqslant 0\]Следовательно, уравнение всегда имеет два (быть может, совпадающих) корня \[t_1=\dfrac{12a+2a+6}2=7a+3\qquad\text{и}\qquad t_2=\dfrac{12a-2a-6}2=5a-3.\]

2) Запишем ответ для \(x\) в общем виде. Пусть \(b\) – корень уравнения \(t^2-12at+35a^2-6a-9=0\). Тогда, сделав обратную замену, получаем \[\log_8(x+a)-\log_8(x-a)=b\quad\Leftrightarrow\quad \begin{cases} \log_8\dfrac{x+a}{x-a}=b\\ x>a\\ x>-a\end{cases}\quad\Leftrightarrow\quad \begin{cases} \left(8^b-1\right)x=a\left(8^b+1\right)\\ x>|a| \end{cases}\]

При \(b=0\) коэффициент \(8^b-1\) перед \(x\) равен нулю, следовательно, уравнение системы примет вид: \(0=2a\). Данное уравнение при \(a=0\) будет иметь бесконечно много решений, при \(a\ne 0\) не будет иметь решений. Следовательно, сама система в каждом случае (после пересечения решения уравнения с ОДЗ \(x>|a|\)) будет иметь либо бесконечное множество решений, либо не иметь решений.
Т.к. случай с бесконечным множеством решений нам не подходит (нам нужно два решения), то \(a\) точно не равно нулю.

Таким образом, мы видим, что при каждом фиксированном \(b\) мы получаем либо одно решение для \(x\) (если \(b\ne 0\)): \[x=a\cdot \dfrac{8^b+1}{8^b-1},\] либо ни одного решения для \(x\) (если \(b=0, a\ne 0\)).
Отсюда можно сделать вывод, что для того, чтобы исходное уравнение имело два решения, нужно, чтобы \(t_1\ne t_2 \quad \text{и}\quad t_1\ne 0,t_2\ne 0\):\[7a+3\ne 5a-3, \ 7a+3\ne 0, 5a-3\ne 0 \quad\Leftrightarrow\quad a\ne -3;\ -\dfrac37; \ \dfrac35,\] а также, чтобы полученные корни для \(x\) удовлетворяли ОДЗ \(x>|a|\).

3) Найдем в общем виде условия, при которых корень \(x=a\cdot\dfrac{8^b+1}{8^b-1}\) удовлетворяет ОДЗ \(x>|a|\). \[a\cdot \dfrac{8^b+1}{8^b-1}>|a| \quad\Rightarrow\quad \left[\begin{gathered} \begin{aligned} &\begin{cases}a> 0\\ \dfrac{8^b+1}{8^b-1}>1\end{cases}\\ &\begin{cases} a<0\\ \dfrac{8^b+1}{8^b-1}<-1\end{cases} \end{aligned} \end{gathered} \right. \quad\Leftrightarrow\quad \left[\begin{gathered} \begin{aligned} &\begin{cases}a> 0\\ b>0\end{cases}\\ &\begin{cases} a<0\\ b<0\end{cases} \end{aligned} \end{gathered} \right.\]

4) Подставим наши корни \(t_1=7a+3\) и \(t_2=5a-3\) вместо \(b\):

\[\left[\begin{gathered} \begin{aligned} &\begin{cases}a> 0\\ 7a+3>0\end{cases}\\ &\begin{cases} a<0\\ 7a+3<0\end{cases} \end{aligned} \end{gathered} \right.\quad\Leftrightarrow\quad a\in \left(-\infty;-\frac37\right)\cup(0;+\infty)\] и \[\left[\begin{gathered} \begin{aligned} &\begin{cases}a> 0\\ 5a-3>0\end{cases}\\ &\begin{cases} a<0\\ 5a-3<0\end{cases} \end{aligned} \end{gathered} \right.\quad\Leftrightarrow\quad a\in (-\infty;0)\cup\left(\frac35;+\infty\right).\]

Пересекая данные решения между собой и с \(a\ne -3;\ -\frac37; \ \frac35\) (найденные во 2-ом пункте), получим окончательный ответ \[a\in (-\infty;-3)\cup\left(-3;-\frac37\right)\cup\left(\frac35;+\infty\right).\]

Ответ:

\(a\in (-\infty;-3)\cup\left(-3;-\frac37\right)\cup\left(\frac35;+\infty\right)\)

Рассмотрим две функции \(f(x)=4|x+3|+3|x-a|\) и \(h(y)=\sqrt{16-y^2}+2\).

Заметим, что при \(x<-3\) модуль \(|x+3|=-x-3\), а при \(x>-3\) модуль \(|x+3|=x+3\). Следовательно, вне зависимости от того, как раскроется модуль \(|x-a|\), при \(x<-3\) коэффициент перед \(x\) у функции \(f(x)\) будет отрицательным (а именно -7 или -1), а при \(x>-3\) он будет положительным (а именно 1 или 7). Следовательно, \(f(x)\) имеет минимум в точке \(x=-3\). Это значит, что \(f(x)\geqslant f(-3)\) при всех \(x\).

Так как \(y^2\geqslant 0\) при всех \(y\) и по ОДЗ \(16-y^2\geqslant 0\), то \(\sqrt{0}\leqslant \sqrt{16-y^2}\leqslant \sqrt{16}\), значит, функция \(h(y)\in [2;6]\) при всех \(y\).
Таким образом, если \(f(-3)>6\), то неравенство \(f(x)\leqslant h(y)\) не имеет решений, так как левая часть больше \(6\), а правая – меньше или равна \(6\).
Следовательно, \(f(-3)\leqslant 6\). При этом нам подходит как минимум одна пара чисел: \(x=-3\) и \(y=0\) (Проверьте!).
Так как \(f(-3)=3|-3-a|=3|a+3|\), то получаем: \[3|a+3|\leqslant 6\quad\Leftrightarrow\quad a\in [-5;-1].\]

Ответ:

\([-5;-1]\)