Задачи на нахождение касательной (страница 2)

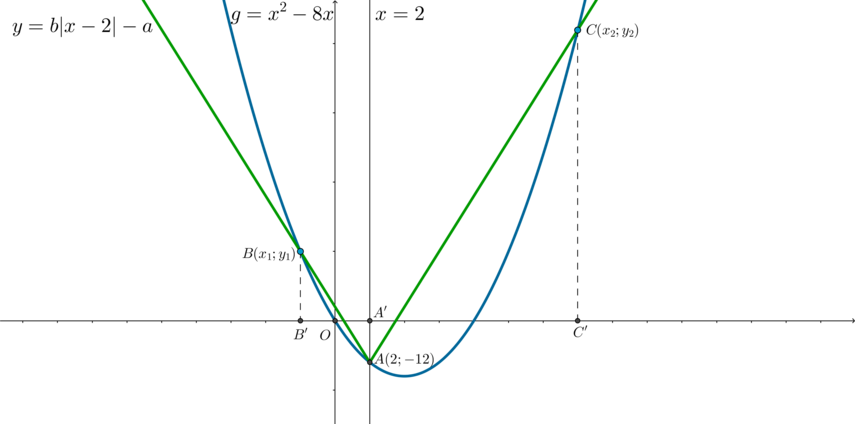
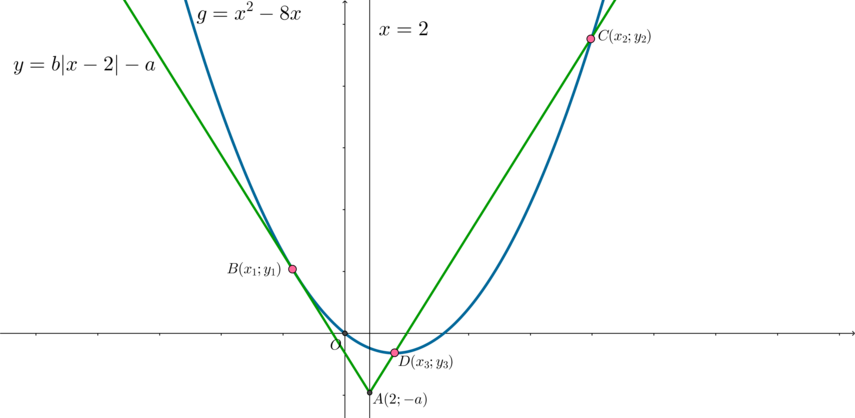
Рассмотрим функции \(f(x)=|x^2-2x-3|\) и \(g(x)=|x-a|+2a\). Тогда уравнение примет вид: \[f(x)=g(x)\] Следовательно, нужно найти значения параметра, при которых графики функций \(f\) и \(g\) будут иметь ровно 2 точки пересечения.

1) Заметим, что графиком \(g\) при каждом фиксированном \(a\) является уголок, вершина которого находится на прямой \(y=2x\).
Найдем \(a\), при котором левая ветка уголка будет касаться графика \(f\) в точке \(A\). Тогда при всех \(a\), больших найденного значения, графики будут иметь ровно 2 точки пересечения.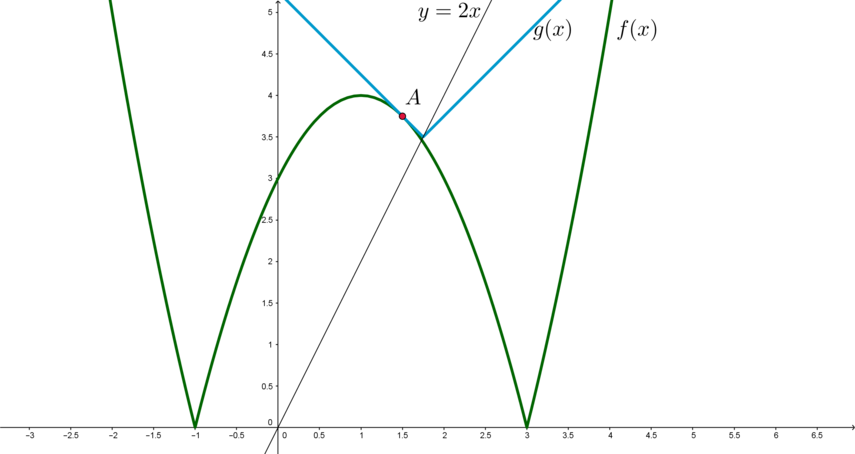



Левая ветка уголка задается уравнением \(y_l=-x+a+2a=-x+3a\), \(x\leqslant a\). Касаться она будет графика функции \(f_1=-x^2+2x+3\).
\(f_1'=-2x+2\). Если \(A(x_0;y_0)\) – точка касания, то \[\begin{cases} -2x_0+2=-1\\ y_0=-x_0^2+2x_0+3 \end{cases} \quad\Leftrightarrow\quad \begin{cases} x_0=\dfrac32\\[1ex] y_0=\dfrac{15}4 \end{cases}\] Так как \(A\in y_l\), то отсюда можно найти \(a\): \[\dfrac{15}4=-\dfrac32+3a\quad\Leftrightarrow\quad a=\dfrac74\] Следовательно, \(a\in \left(\frac74;+\infty\right)\).

2) Найдем значения \(a\), когда \(g\) проходит через точку \(B(-1;0)\) (положение \(I\)) и через точку \(C(3;0)\) (положение \(II\)).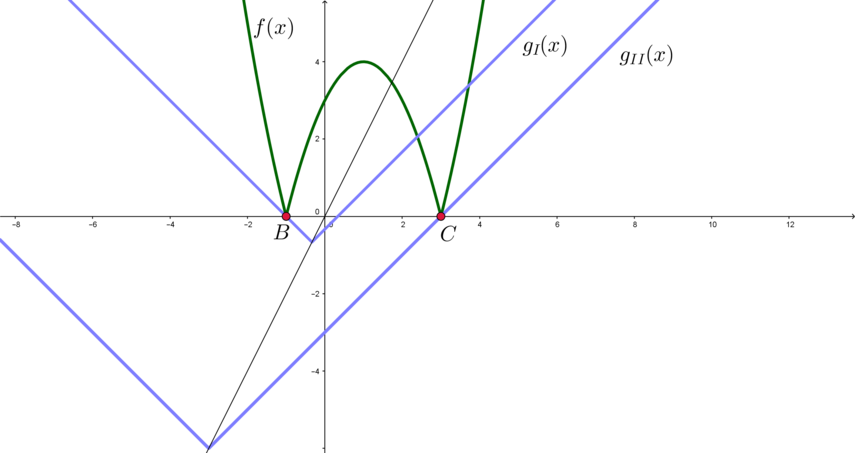



Заметим, что если \(g\) находится между положениями \(I\) и \(II\), то она имеет с \(f\) также ровно 2 точки пересечения.
Для положения \(I\) (левая ветка уголка проходит через \(B\)): \[0=1+3a \quad\Leftrightarrow\quad a=-\dfrac13\] Для положения \(II\) (правая ветка уголка \(y_p=x+a\) проходит через \(C\)): \[0=3+a \quad\Leftrightarrow\quad a=-3.\] Следовательно, \(a\in \left(-3;-\frac13\right)\).

Ответ:

\(a\in \left(-3;-\frac13\right)\cup\left(\frac74;+\infty\right)\)

Неравенство системы задает круг без границы с центром в точке \((0;3)\) и радиусом \(2\).
Обозначим \(2a=b\).
Заметим, что при \(b\leqslant 0\) система не имеет решений (ветви параболы направлены вниз или \(y=0\)). Следовательно, \(b>0\).

Для того, чтобы система имела хотя бы одно решение, нужно, чтобы парабола пересекала данный круг (без границы).
Найдем граничные случаи: когда парабола касается окружности \(x^2+(y-3)^2=4\).
Пусть \(x_0\) – точка касания. Тогда в этой точке парабола и окружность имеют общую касательную \(y=kx+b\).
Заметим, что рисунок симметричен относительно оси ординат, следовательно, рассмотрим только правую часть рисунка (где \(x>0\)).
Пусть \(B(x_0;y_0)\) – точка касания, \(A\) – точка пересечения касательной с осью ординат, \(Q\) – точка пересечения касательной с осью абсцисс, \(O\) – радиус окружности, \(D\) – начало координат.
Тогда уравнение касательной выглядит так: \(y_k=2bx_0\cdot x-bx_0^2\). Тогда \(A(0;-bx_0^2), \ B(x_0;bx_0^2), \ Q\left(\frac{x_0}2; 0\right)\).
Тогда \(OB\perp AB\) как радиус, проведенный в точку касания. Следовательно, \(\triangle ADQ\sim \triangle ABO\): \[\dfrac{DQ}{OB}=\dfrac{AQ}{AO} \quad (*)\] \(DQ=\frac{x_0}2\), \(OB=2\), \(AO=3+bx_0^2\). Найдем \(AQ\) по теореме Пифагора: \[AQ=\dfrac{\sqrt{4b^2x_0^2+1}}2x_0\] Теперь подставим все значения в \((*)\) и получим уравнение: \[4(4b^2x_0^2+1)=(3+bx_0^2)^2 \quad (1)\] Так как точка \(B\) также принадлежит окружности, то можно составить второе уравнение: \[x_0^2+(bx_0^2-3)^2=4\quad (2)\] Решая систему из двух полученных уравнений \((1)\) и \((2)\) относительно \(b\) и \(x_0\), находим, что \[b=\dfrac{3\pm \sqrt5}8>0\] Так как в нашем случае при \(x>0\) существует ровно одна точка касания окружности и параболы, то одно из двух значений, найденных для \(b\), не подойдет (не будет существовать \(x_0>0\)). Проверим \(b=\frac{3+\sqrt5}8\). Подставим его в уравнение \((2)\): \[(7+3\sqrt5)x_0^4-8(5+3\sqrt5)x_0^2+5\cdot 32=0\] Если рассматривать это уравнение как квадратное относительно \(x_0^2\), то дискриминант уравнения равен \[D=64(5+3\sqrt5)^2-4\cdot 32\cdot 5(7+3\sqrt5)=0\] Следовательно, единственный корень \[x_0^2=\dfrac{8(5+3\sqrt5)}{2(7+3\sqrt5)}=6\sqrt5-10>0\] Таким образом, при данном \(b\) существует \(x_0=\sqrt{6\sqrt5-10}\).

Следовательно, \(b=\frac{3-\sqrt5}8\) не подойдет (можно убедиться в этом, сделав аналогичную проверку).
Так как рисунок, как замечалось ранее, симметричен относительно оси ординат, то касание в точке \(C\) будет возможно также при \(b=\frac{3+\sqrt5}8\). Следовательно, значения для \(b\), при которых система будет иметь решения, это \[b\in \left(\dfrac{3+\sqrt5}8; +\infty\right) \quad \Rightarrow\quad a\in \left(\dfrac{3+\sqrt5}{16};+\infty\right)\]

Скобки круглые, потому что круг без границы.

Ответ:

\(a\in \left(\dfrac{3+\sqrt5}{16};+\infty\right)\)

Перепишем уравнение в виде \[x^2-8x=b|x-2|-a\] и рассмотрим функцию \(g=x^2-8x\) и \(y=b|x-2|-a\). Графиком функции \(g\) является парабола, ветви которой направлены вверх, а пересекает ось абсцисс она в точках \(x=0\) и \(x=8\). Графиком \(y\) при каждом фиксированном \(b\) и \(a\) является уголок, вершина \((2;y_0)\) которого находится на прямой \(x=2\).
Точка, в которой парабола пересекает \(x=2\), имеет координаты \(A(2;-12)\).
Заметим, что если вершина уголка находится выше этой точки (то есть \(y_0>-12\)), то \(y\) с \(g\) не будут иметь 3 точки пересечения.

1) Рассмотрим случай, когда \(y_0=-12\). Тогда \(a=12\).



Заметим, что если ветви уголка направлены вниз (то есть \(b<0\)), а также при \(b=0\), \(y\) не будет пересекать \(g\) в трех точках.
Рассмотрим случай \(b>0\). Тогда мы имеем еще две точки пересечения \(y\) с \(g\): точки \(B\) и \(C\).
Так как точка \(A'\) находится левее \(x=4\) (абсцисса вершины параболы), то \(A'B'<A'C'\). Следовательно, и \(OB'<OC'\). Значит, не может быть \(x_1+x_2=0\), следовательно, только \(x_1+2=0\), откуда \(x_1=-2\). Следовательно, \(g(x_1)=y(x_1)\), то есть \[(-2)^2-8\cdot (-2)=b|-2-2|-12 \quad\Rightarrow\quad b=8.\] Таким образом, получили первое решение \(a=12; b=8.\)

2) Рассмотрим случай, когда \(y_0<-12\), то есть \(a>12\).
Заметим также, что если \(b\leqslant 0\), то \(y\) не будет иметь 3 точки пересечения с \(g\). Следовательно, рассматриваем только случай, когда ветви уголка направлены вверх.
\(y\) будет иметь 3 точки пересечения с \(g\) в одном из двух случаев:
— когда левая ветка уголка касается параболы, а правая пересекает в двух точках (см. второй рисунок);
— когда левая ветка уголка пересекает параболу в двух точках, а правая касается.

a) Рассмотрим первый случай.



Левая ветка уголка задается уравнением \(y_l=b(2-x)-a\), \(x<2\). Следовательно, условие касания: \[\begin{cases} -b=g'(x_1)=2x_1-8\\ g(x_1)=x_1^2-8x_1=b(2-x_1)-a=y_l(x_1) \end{cases} \quad\Leftrightarrow\quad \begin{cases} -b=2x_1-8\\ x_1^2-8x_1=b(2-x_1)-a \end{cases}\] Правая ветка (\(y_p=b(x-2)-a\), \(x>2\)) должна пересекать параболу в точке, абсцисса которой равна \(-x_1>2\) (неизвестно, это точка \(D\) или \(C\)). Это задается условием: \[y_p(-x_1)=b(-x_1-2)-a=(-x_1)^2-8\cdot (-x_1)=g(-x_1)\] Решаем систему из трех уравнений \[\begin{cases} -b=2x_1-8\\ x_1^2-8x_1=b(2-x_1)-a\\ b(-x_1-2)-a=x_1^2+8\cdot x_1 \end{cases} \quad\Leftrightarrow\quad \begin{cases} b=16\\ a=48\\ x_1=-4 \end{cases}\] Проверим эти значения (нам нужно проверить, что правая ветка уголка будет именно в двух точках пересекать параболу).
\(16(x-2)-48=x^2-8x \quad\Rightarrow\quad x_3=4\) и \(x_2=20\).
Таким образом, получен еще один ответ \(a=48\), \(b=16\).

b) Рассмотрим второй случай.



Аналогично получаем систему: \[\begin{cases} b=2x_3-8\\ x_3^2-8x_3=b(x_3-2)-a\\ b(2+x_3)-a=x_3^2+8\cdot x_3 \end{cases} \quad\Leftrightarrow\quad \begin{cases} b=-16\\ a=48\\ x_3=-4 \end{cases}\] Что невозможно, исходя из рисунка (\(x_3>2\)).

Ответ:

\(a=12, b=8\) и \(a=48, b=16\)