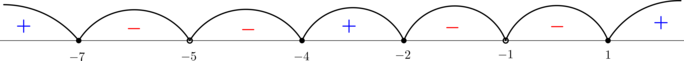Решение неравенств прошлых лет (страница 7)

ОДЗ:

\[\begin{cases} (x+5)^4 > 0\\ (x+4)^2 > 0\\ \dfrac{(x+4)^3}{x+5} > 0\\ x + 5 \neq 0 \end{cases} \qquad\Leftrightarrow\qquad x \in (-\infty; -5)\cup(-4; +\infty).\]

\[\log_{2^2}(x+5)^4\cdot\log_{2^4}(x+4)^2+\log_{2}\dfrac{(x+4)^3}{x+5}-3>0.\] На ОДЗ неравенство равносильно:
\[\log_{2}|x+5|\cdot\log_{2}|x+4|+3\log_{2}|x+4| - \log_{2}|x+5|-3>0.\] Сгруппируем первое и второе слагаемые, а также третье и четвертое:

\[\begin{aligned} &(\log_{2}|x+4| - 1)(\log_{2}|x+5| + 3)>0\qquad\Leftrightarrow\\ \Leftrightarrow\qquad&(\log_{2}|x+4| - \log_22)(\log_{2}|x+5| + \log_{2}8)>0\qquad\Leftrightarrow\\ \Leftrightarrow\qquad&\log_{2}\dfrac{|x+4|}{2}\cdot\log_{2}(8\cdot|x+5|)>0. \end{aligned}\]

Возможны 2 случая:
1)

\[\begin{cases} \log_{2}\dfrac{|x+4|}{2} > 0\\ \log_{2}(8\cdot|x+5|) > 0\\ \end{cases}\]

В этом случае по методу рационализации: \(|x + 4| > 2, \ |x + 5| > \dfrac{1}{8}\), откуда
\(x\in(-\infty; -6)\cup(-2; +\infty)\).
2)

\[\begin{cases} \log_{2}\dfrac{|x+4|}{2} < 0\\ \log_{2}(8\cdot|x+5|) < 0\\ \end{cases}\]

В этом случае по методу рационализации: \(|x + 4| < 2, \ |x + 5| < \dfrac{1}{8}\), откуда
\(x\in(-5,125; -4,875)\).
Объединенное решение неравенства: \(x\in(-\infty; -6)\cup(-5,125; -4,875)\cup(-2; +\infty)\).
Пересечем ответ с ОДЗ: \(x \in (-\infty; -6)\cup(-5,125; -5)\cup(-2; +\infty)\).
Окончательный ответ \[x \in (-\infty; -6)\cup(-5,125; -5)\cup(-2; +\infty).\]

Ответ:

\((-\infty; -6)\cup(-5,125; -5)\cup(-2; +\infty)\)

ОДЗ:

\[\begin{cases} x + 3 \neq 0\\ \dfrac{x+5}{x+3} > 0\\ (x+1)^2 > 0 \end{cases} \qquad\Leftrightarrow\qquad x \in (-\infty; -5)\cup(-3; -1)\cup(-1; +\infty)\]

\[\begin{aligned} &\log_33-\log_{3}\dfrac{x+5}{x+3}\geqslant\dfrac{1}{2}\log_{3}(x+1)^2\quad\Leftrightarrow\quad \log_{3}\dfrac{3(x+3)}{x+5}\geqslant\dfrac{1}{2}\log_{3}(x+1)^2\quad\Leftrightarrow\\ &\Leftrightarrow\quad \log_{3}\dfrac{9(x+3)^2}{(x+5)^2}\geqslant\log_{3}(x+1)^2\quad\Leftrightarrow\quad \log_{3}\dfrac{9(x+3)^2}{(x+5)^2(x+1)^2}\geqslant 0. \end{aligned}\]

По методу рационализации это неравенство на ОДЗ равносильно:

\[\begin{aligned} &(3 - 1)\left(\dfrac{9(x+3)^2}{(x+5)^2(x+1)^2} - 1\right)\geqslant 0\quad\Leftrightarrow\quad \dfrac{9(x+3)^2 - (x+5)^2(x+1)^2}{(x+5)^2(x+1)^2}\geqslant 0\quad\Leftrightarrow\\ &\Leftrightarrow\quad \dfrac{(3x+9 - (x+5)(x+1))(3x+9 + (x+5)(x+1))}{(x+5)^2(x+1)^2}\geqslant 0\quad\Leftrightarrow\\ &\Leftrightarrow\quad \dfrac{(-x^2 - 3x + 4)(x^2 + 9x + 14)}{(x+5)^2(x+1)^2}\geqslant 0\quad\Leftrightarrow\quad \dfrac{(x^2 + 3x - 4)(x^2 + 9x + 14)}{(x+5)^2(x+1)^2}\leqslant 0\quad\Leftrightarrow\\ &\Leftrightarrow\quad \dfrac{(x + 4)(x - 1)(x + 7)(x + 2)}{(x+5)^2(x+1)^2}\leqslant 0 \end{aligned}\]

По методу интервалов:



откуда \(x \in[-7; -5)\cup(-5; -4]\cup[-2; -1)\cup(-1; 1]\).
Пересечем ответ с ОДЗ: \(x \in [-7; -5)\cup[-2; -1)\cup(-1; 1]\).
Окончательный ответ \[x \in [-7; -5)\cup[-2; -1)\cup(-1; 1].\]

Ответ:

\([-7; -5)\cup[-2; -1)\cup(-1; 1]\)